名师点拨小升初奥数知识及学习方法
在重庆小升初择校过程中,奥数是重头戏,几乎重庆的重点中学都以学生的奥数成绩为择生标准,所以奥数的学习很大程度上决定着择校的成败。怎样在小升初奥数考试中拿得高分,取得小升初择校的最终胜利呢,下面就来看看奥数名师总结的小升初奥数知识及学习方法。
一、为什么学习奥数?
1.培养数学思维、开发智力
奥数作为数学上比较有难度的一部分,很能开阔学生的思维,由于奥数相对于课本教学在难度上的提升以及对孩子思维的引导,一般情况下在学习一段时间奥数后孩子在学校的数学成绩会非常优异,数学成绩优异了能提升孩子对数学的兴趣,兴趣能为孩子以后长久的数学学习建立起主观上的能动性来,同时兴趣也是学好奥数必不可少的前提条件。
2.使学生获得心里上的优势,增强自信
小孩子因为年龄上心理上都还很稚嫩,因此,比较容易受到情绪影响。如果总是遇到挫折就会对一件事物失去兴趣,但是如果总是获得成功就会兴趣大增。在奥数的学习上,“成就感”就是一个关键的理念,让孩子在奥数的学习和运用过程中体会到乐趣,获得成就感,慢慢就会越来越喜欢学习。
3.对于初中数理化的学习有很大的帮助
奥数很大的作用在于有利于学生提前接触相关的物理、化学等知识,在在升入初中以后,孩子学习数理化就不再很陌生,学起来更加容易。
二、小学奥数知识体系
小学的奥数的几个重要模块主要是计算模块、数论模块、几何模块、行程模块、应用题模块、杂题模块。
| 计算模块 | 数论模块 | 几何模块 | 行程模块 | 应用题模块 | 杂题 |
| 1.速算与巧算 2.分数小数四则混合 运算及繁分数运算 3.循环小数化分数与 混合运算 4.等差及等比数列 5.计算公式综合 6.分数计算技巧之裂项、 换元、通项归纳 7.比较与估算 8.定义新运算 9.解方程 | 1.质数与合数 | 直线型: 1.长度与角度 2.格点与割补 3.三角形等积变换 与一半模型 4.勾股定理与弦图 5.五大模型 曲线型: 1.圆与扇形的周长与 面积 2.图形旋转扫过的面 积问题 立体几何: 1.立体图形的面积与 体积 2.平面图形旋转成的 立体图形问题 3.平面展开图 4.液体浸物问题 | 1.简单相遇与追 及问题 2.环形跑道问题 3.流水行船问题 4.火车过桥问题 5.电梯问题 6.发车间隔问题 7.接送问题 8.时钟问题 9.多人相遇与追 及问题 10.多次相遇追及 问题 11.方程与比例法解行程问题 | 1.列方程解应用题 2.分数、百分 数应用题 3.比例应用题 4.工程问题 5.浓度问题 6.经济问题 7.牛吃草问题 | 1.从简单情况入手 2.对应与转化思想 3.从反面与从特殊 情况入手思想 4.染色与覆盖 5.游戏与对策 6.体育比赛问题 7.逻辑推理问题 8.数字谜 9.数独 …… |
三、奥数学习方法指导
学生需要知道的完美学习规划
多做杯赛及小升初试题,多做奥数基础训练题、每日一题,特别是杯赛类真题很重要,保证奥数试题的熟悉度。
学习时要思考,反思自己的思维过程,反思知识点和解题技巧,反思多种解法的优劣,反思各种方法的纵横联系。
及时巩固练习,课堂及奥数试题下来以后一定要及时巩固练习,保证知识的牢靠性。
定期回顾复习,回顾练习是必不可少的,除了当时下来的练习,后期要针对模块定期回顾。
善于归纳总结,总结出它所用到的数学思想方法,并把思想方法相近的题目编成一组,不断提炼、不断深化,做到举一反三、触类旁通。
保证学过的都会做,奥数学习之后一定要经常练习,至少要保证学过的都会做。
家长需要知道的家庭教育要收放自如
积极鼓励,一项调查发现,鼓励人有利于提高人的自信心,因而做事也能事半功倍,在小升初孩子学习的过程中,家长也要适当鼓励孩子,提示孩子自己很能干。
适时收手,家长也要学会放手,让孩子自己主动的思考,自己做决定,让孩子的思维得到自由的发挥。
细心观察,家长及时和教师联系了解自己孩子的情况,以便知道课下的努力方向和方法。系统检查一下孩子的作业、单元测试、考试卷、奥数练习等,从中也可以发现孩子易出错的地方,找出他的弱项。
耐心引导,我们应该在不引起孩子反感的情况下,检查并适当督促其完成家庭作业。同时,注意调整孩子的心态,培养孩子积极、健康、上进的心态,是您给他(她)是一生最宝贵的财富。
知识牵引的体验式学习—换元之旅
闯关1:
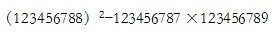
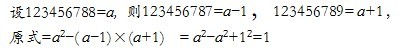
闯关2:98764×88765-98765×88764
解析:设98764=a,88764=b,则98765=a+1, 88765=b+1
原式=a×(b+1)-( a+1)×b=ab+a-ab-b=a−b
=98764−88764=10000
闯关3:2009×20082007−2007×20082009
设2007=a,20082007=b
原式=(a+2)×b−a×(b+2)
=ab+2b−ab−2a
=2×(b−a)
=2×(20082007−2007)
=40160000
闯关4:(7.88+6.77+5.66)×(9.31+10.98+10)− (7.88+6.77+5.66+10)×(9.31+10.98)
设a= 7.88+6.77+5.66,b= 9.31+10.98
原式=a×(b+10)−(a+10)×b
=ab+10a−ab −10b
=10(a−b)
=10×(7.88+6.77+5.66−9.31−10.98)
=10−0.02
=0.2