小升初奥数题型解析:植树问题(二)

同学们，植树问题，其实就是数学中设置等分点的计算问题。因此题中的情节不局限于植树，生活中的跨楼梯，锯木头，插红旗，安路灯等问题，都可以按照植树问题的数量关系和思路解答。

(一)典型例题

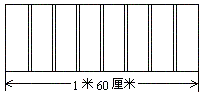
例1. 有一个窗框长1米60厘米，准备安装7根铁栏杆，栏杆的距离是多少厘米?

分析与解答：

观察下图不难发现，7根铁栏杆把窗框平均分成8段，我们只要把1米60厘米平均分成8份就可以了。

(1)先求有多少个间隔?

7+1=8(个)

(2)再求栏杆间的距离

1米60厘米=160厘米

160÷8=20(厘米)

答：栏杆的距离是20厘米。

例2. 时钟5点钟敲5下，8秒钟敲完，那么10点钟敲10下，需要多少秒?

分析与解答：

时钟5点钟敲5下，其中有4个间隔，4个间隔用8秒钟的时间，就可以求出每一个间隔所用的时间。然后再想，10点钟敲10下，有9个间隔，就可以求出所需要的时间了。

(1)先求5下有几个间隔

5-1=4(个)

(2)再求每一个间隔的时间

8÷4=2(秒)

(3)再求10下有几个间隔

10-1=9(个)

(4)最后求需几秒钟

2×9=18(秒)

综合算式：8÷(5-1)×(10-1)=18(秒)

答：需要18秒钟。

例3. 在一个正方形池塘四周栽树，四个顶点各栽一棵，这样每边都栽有25棵，如果每相邻两棵之间相距2米，这个正方形池塘的周长有多少米?

分析与解答：

这道题有两种解答方法，一种是先求一共有多少棵树，再求周长;另一种是先求正方形的边长，再求周长。

解法一：

(1)先求一共有多少棵树

25×4-4=96(棵)

或：(25-1)×4=96(棵)

(2)再求池塘的周长

2×96=192(米)

解法二：

(1)先求池塘的边长

2×(25-1)=48(米)

(2)再求池塘的周长

48×4=192(米)

答：池塘的周长有192米。

例4. 长3米的钢管，从一端开始，先30厘米锯一段，再20厘米锯一段，这样长短交替锯成小段，可锯成30厘米长的有多少段?20厘米长的有多少段?若每锯一段用8分钟，锯完一段休息2分钟，全部锯完需用多少分钟?

分析与解答：

先把3米换算成300厘米，先可以求出把300厘米的长的木棍锯成50厘米的一段，再把每一个50厘米锯成2段，需要6次，共锯11次，休息10次。

3米=300厘米

20+30=50(厘米)

300÷50=6段

6×2-1=11(次)(锯11次，休息10次)

11×8+10×2=108(分钟)

答：锯成30厘米的共6段，锯成20厘米的6段，锯完共需108分钟。

(二)试一试，独立完成

1. 有一个窗框长2米，准备在窗框中间等距离地装9根铁栏杆，相邻的两根铁栏杆距离是多少厘米?

2. 在长90米的跑道两侧插14面彩旗，每相邻两面粉旗之间长多少米?

3. 在小河的一旁，从头到尾要植561棵柳树，已知每隔3米植1棵，那么这条小河长多少米?

4. 在一条长5千米的公路一侧安电线杆，每隔50米安一根，连两端在内一共需装多少根?

(三)解决生活中实际问题

1. 一条路的一侧有37棵树，两树的间隔是5米，现在路的一侧以6米的距离安装路灯，共需要多少盏灯?

2. 把一根木头锯成10段，每锯一段需用7分钟，需几分钟?

3. 一座15层楼，每层的台阶数都相等，小红从一层到3层共走了48个台阶，小红从一层走到15层共需迈多少台阶?