2011年“世奥赛”复赛答案及解析

上周末，12月24日下午，郑州进入“世奥赛”复赛的孩子都在商专进行了考试。小编现将此次的复赛的试卷，以及初赛和初赛加试题整理如下，供大家学习。前面小编为大家整理了2011年世界少年奥林匹克数学竞赛的初赛、初赛加试和复赛试题。

论坛的狮子老师为大家解析除了答案，还有详细解析，小编整理如下，供大家参考。下面是世奥赛复赛的答案及解析，初赛答案及解析敬请期待狮子老师的详解。

下面文章中为真题和解析预览。答案和详解，请大家点击下载下图的可打印版文档，进行查看。

1、（10分）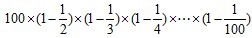

解析：分数计数

答案：1

2、(10分）比较大小（１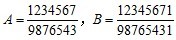）（２）

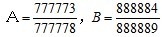
解析：分数比较大小

（1）A分子分母同时扩大十倍，取A-B。A＜B

（2）化简A、B。

A＜B

3、（10分）有甲、乙、丙三个装有汽油的木桶，如果把甲桶内的1/3的油倒入乙桶，再把乙桶内1/4的油倒入丙桶，最后把丙桶内的1/7的油倒入甲桶，这时三桶内的油都是12升，求每个桶内原有汽油多少升？

解析：应用题

从上面两个式子，我们求得丙=10（升）、甲=15（升）、乙=11（升）

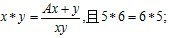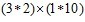4、（10分）规定求的值。

解析：定义新运算

根据5*6=6*5，求出A=1.所以x*y=

3*2=（3+2）/6 1*10=（1+10）/10

=

5、（10分）一个圆柱形玻璃容器的底面直径是10厘米。把一块铁块从这个容器的水中取出后，水面下降2厘米，这块铁块的体积是多少？（）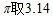

解析：几何体积

铁块体积：

6、（10分）某旅游团体准备订购定价为100元的某种纪念章80枚。团体负责人对商店经理说：“如果你肯降价，那么每降价1元，我就多订购4枚。”商店经理算了一下，若降价5%，则由于旅游团体多订购，获得的利润反而比原来多100元，这种纪念章的成本是多少元？

解析：应用题利润问题（同一中数学邀请赛初赛试题一样）

设成本为a，降价5%，价格减少了5元。团体负责人会多买5*4=20枚。

求得：a=70

7、（10分）已知一容器内装有10升纯酒精，倒出３升后用水加满，然后再倒出3.5升，再加满水。问：这时溶液的浓度是多少？

解析：应用题浓度问题

第一次加满水后的浓度为：

倒出3.5升后，容器内还剩下酒精：

所以此时溶液浓度为：

答案：45.5%

8、（10分）某项工作，如果甲先单独做45天，再由乙单独做18天可以完成；如果甲、乙合作30天也可以完成；现在由甲先单独做20天，问乙还需要做多少天才能完成这项工作？

解析：应用题工程问题

甲先单独做45天，再由乙单独做18天可以完成，可以理解为：甲乙合做18天，甲再做27天。

甲乙合做18天完成总工程的：

甲的工作效率：

乙的工作效率：

甲先单独做20天，乙还需要：（天）

------------------------------------------------------------------------------------

9、（10分）图中长方形内画了一些直线，已知边上有三块面积分别是15，34，47，求图中阴影部分的面积是多少。

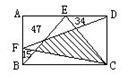
解析：一半模型

答案：15+34+47=96

10、（10分）将440拆分为11个自然数的和，使这11个自然数从小到大排成一行后，相邻两个数的差都是５.求第１个数和第９个数分别是几？

解析：数论问题

设最小的那个数为a，则这11个自然数分别为：a、a+5、a+10、…、a+50

根据题意：11a+5*（1+2+3+…+10）=440

求得：a=15

所以第一个数：a=15 第9个数：15+5*8=55

11、（10分）某公司在A、B两地分别库存有某机器16台和12台，现要运往甲、乙两家客户的所在地，其中甲方15台，乙方13台。已知从A地运一台到甲方的运费为500元，到乙方的运费为400元，从B地运一台到甲方的运费为300元，到乙方的运费为600元。已知运费由公司承担，公司应设计怎样的调运方案，才能使这些机器的总运费最省？费用最少是多少？

解析：杂题统筹规划问题

B地机器全部运送到甲地：12*300=3600

A地机器分开运送，甲地3台：3*500=1500，乙地13台：13*400=5200

所以费用为：3600+1500+5200=10300（元）

12、（10分）一次数学竞赛，准备了22支铅笔作为奖品发给一、二、三等奖的学生，原计划发给一等奖每人6支，二等奖每人3支，三等奖每人2支，后来改为一等奖每人9支，二等奖每人4支，三等奖每人1支，总支数仍是22支。问：获一、二、三等奖的学生各多少名？

解析：求解不定方程

设一等奖x，二等奖y，三等奖z

6x+3y+2z=22①

9x+4y+z=22②

②×2－①得

12x＋5y＝22

x为整数只能为1

y=2 z=5

则一、二、三等奖的学生各有：1、2、5名。

13、（10分）甲、乙、丙三队要完成A、B两项工程。B工程的工作量比A工程的工作量多1/4。甲、乙、丙三队单独完成A工程所需要的时间分别是20天、24天、30天。为了同时完成这两项工程，先派甲队做A工程，乙、丙两队共同做B工程；经过几天后，又调丙队与甲队共同完成A工程。丙队与乙队合做了多少天？

解析：应用题工程问题

设乙丙合作a天。

求解a=15（天）

14、（10分）汽车在南北走向的公路上行驶时，由南向北逆风而行，每小时50千米；由北向南顺风而行，每小时行70千米。两辆汽车同时从同一地点出发相背而行，一辆汽车往北驶去然后返回，另一辆汽车往南驶去然后返回，结果4小时后，两车同时回到出发点。如果掉头时间不计，在这4小时内两车行驶的方向相同的有多少小时？

解析：行程问题

两辆汽车从出发点出发时速度比：5:7

两车相背而行路程分别为：5/12 7/12

路程差就是两车行驶方向相同：7/12-5/12=1/6

所以两车行驶方向相同的时间为：4*1/6=2/3

更多分享及讨论请点击查看：12月24日世界少年奥林匹克数学竞赛六年级试题

最后，预祝郑州小升初的同学们都能取得优异的成绩，进入理想的中学！

------------------------------------------------------------------------------------