小学数学奥林匹克模拟试卷（5）

一、填空题：

1.一个学生用计算器算题，在最后一步应除以10，错误的乘以10了，因此得出的错误答数500，正确答案应是______.

2.把0，1，2，…，9十个数字填入下面的小方格中，使三个算式都成立：

□+□=□

□-□=□

□×□=□□

3.两个两位自然数，它们的最大公约数是8，最小公倍数是96，这两个自然数的和是______.

4.一本数学辞典售价a元，利润是成本的20％，如果把利润提高到30％，那么应提高售价______元。

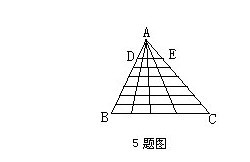
5.图中有______个梯形。

6.小莉8点整出门，步行去12千米远的同学家，她步行速度是每小时3千米，但她每走50分钟就要休息10分钟。则她______时到达。

7.一天甲、乙、丙三个同学做数学题。已知甲比乙多做了6道，丙做的是甲的2倍，比乙多22道，则他们一共做了______道数学题。

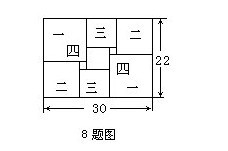
8.在右图的长方形内，有四对正方形（标号相同的两个正方形为一对），每一对是相同的正方形，那么中间这个小正方形（阴影部分）的面积为______.

9.有a、b两条绳，第一次剪去a的2/5，b的2/3；第二次剪去a绳剩下的2/3，b绳剩下的2/5；第三次剪去a绳剩下的2/5，b绳的剩下部分的2/3，最后a剩下的长度与b剩下的长度之比为2∶1，则原来两绳长度的比为______.

10.有黑、白、黄色袜子各10只，不用眼睛看，任意地取出袜子来，使得至少有两双袜子不同色，那么至少要取出______只袜子。

二、解答题：

1.字母A、B、C、D、E和数字1997分别按下列方式变动其次序：

B C D E A 9 9 7 1（第一次变动）

C D E A B 9 7 1 9（第二次变动）

D E A B C 7 1 9 9（第三次变动）

……

问最少经过几次变动后ABCDE1997将重新出现？

2.把下面各循环小数化成分数：

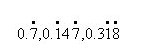
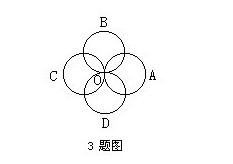
3.如图所示的四个圆形跑道，每个跑道的长都是1千米，A、B、C、D四位运动员同时从交点O出发，分别沿四个跑道跑步，他们的速度分别是每小时4千米，每小时8千米，每小时6千米，每小时12千米。问从出发到四人再次相遇，四人共跑了多少千米？

4.某路公共汽车，包括起点和终点共有15个车站，有一辆车除终点外，每一站上车的乘客中，恰好有一位乘客到以后的每一站下车，为了使每位乘客都有座位，问这辆公共汽车最少要有多少个座位？

参考答案：

一、填空题：

1.（5）

500÷10÷

2.（1+7=8，9-3=6，4×5=20）

首先考虑0只能出现在乘积式中。即分析2×5，4×5，5×6，8×5几种情况。最后得以上结论。

3.（56）

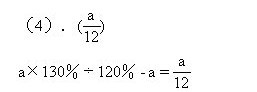
96÷8=12=3×4，所以两个数为8×3=24，4×8=32，和为32+24=56.

梯形的总数为：BC上线段总数×BD上线段总数，即（4+3+2+1）×（6+5+4+3+2+1）

6.（中午12点40分）

3千米/小时=0.05千米/分，0.05×50=2.5千米，即每小时她走2.5千米。12÷2.5=4.8，即4小时后她走4×2.5=10千米。（12-10）÷0.05=40（分），最后不许休息，即共用4小时40分。

7.（58）

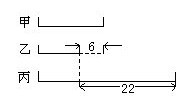
画图分析可得22-6=16为甲做题数，所以可得乙10道，丙16×2=32道，一共16+10+32=58（道）。

8.（36）

长方形的宽是“一”与“二”两个正方形的边长之和。长方形的长是“一”、“二”、“三”三个正方形的边长之和。长-宽=30-22=8是“三”正方形的边长。宽又是两个“三”正方形与中间小正方形的边长之和，因此中间小正方形边长=22-8×2=6，中间小正方形面积=6×6=36.

9.（10∶9）

10.（13）

考虑最坏的情形，把某一种颜色的袜子全部先取出，然后，在剩下两色袜子中各取出一只，这时再任意取一只都必将有两双袜子不同色，即10+2+1=13（只）。

二、解答题：

1.（20）

由变动规律知，A、B、C、D、E经5次变动重新出现，而1997经过4次即重新出现，故要使ABCDE1997重新出现最少需20次（即4和5的最小公倍数。）

3.（15千米）

4.（56个）

本题可列表解。除终点，我们将车站编号列表：

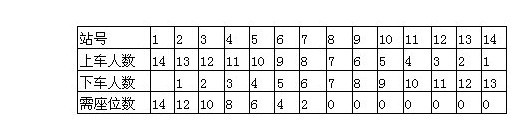
共需座位：

14+12+10+8+6+4+2=56（个）