小学数学奥林匹克模拟试卷（11）

一、填空题：

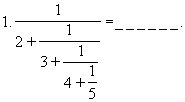
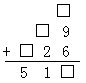
2.下面三个数的平均数是170，则圆圈内的数字分别是：

○；○9；○26.

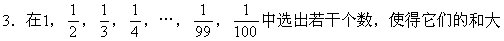于3，至少要选______个数。

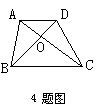
4.图中△AOB的面积为15cm2，线段OB的长度为OD的3倍，则梯形ABCD的面积为______.

5.有一桶高级饮料，小华一人可饮14天，若和小芳同饮则可用10天，若小芳独自一人饮，可用______天。

6.在1至301的所有奇数中，数字3共出现_______次。

7.某工厂计划生产26500个零件，前5天平均每天生产2180个零件，由于技术革新每天比原来多生产420个零件，完成这批零件一共需要_______天。

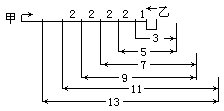
8.铁路与公路平行。公路上有一个人在行走，速度是每小时4千米，一列火车追上并超过这个人用了6秒。公路上还有一辆汽车与火车同向行驶，速度是每小时67千米，火车追上并超过这辆汽车用了48秒，则火车速度为______，长度为______.

9.A、B、C、D4个数，每次去掉一个数，将其余3个数求平均数，这样计算了4次，得到下面4个数：23，26，30，33，A、B、C、D4个数的平均数是______.

10.一个圆的周长为1.26米，两只蚂蚁从一条直径的两端同时出发沿圆周相向爬行。这两只蚂蚁每秒分别爬行5.5厘米和3.5厘米。它们每爬行1秒，3秒，5秒，……（连续奇数），就调头爬行。那么，它们相遇时，已爬行的时间是______秒。

二、解答题：

1.小红见到一位白发苍苍的老爷爷，她问老爷爷有多大年岁？老爷爷说：把我的年龄加上10用4除，减去15后用10乘，结果正好是100岁。请问这位老爷爷有多大年龄？

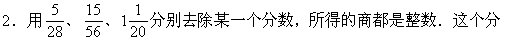数最小是几？

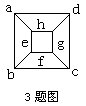
3.下图中8个顶点处标注数字a，b，c，d，e，f，g，h，其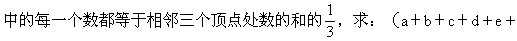

＋g＋h）的值。

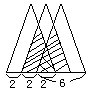
4.底边长为6厘米，高为9厘米的等腰三角形20个，迭放如下图：

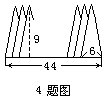
每两个等腰三角形有等距离的间隔，底边迭合在一起的长度是44厘米。回答下列问题：

（1）两个三角形的间隔距离；

（2）三个三角形重迭（两次）部分的面积之和；

（3）只有两个三角形重迭（一次）部分的面积之和；

（4）迭到一起的总面积。

一、填空题：

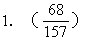
2.（5，7，4）

由总数量÷总份数=平均数，可知这三个数之和170×3=510.

这样，一位数是5.两位数的十位数是7.三位数的百位数是

3.（11个）

要使所选的个数尽可能的少，就要尽量选用大数，而所给的数是从大到

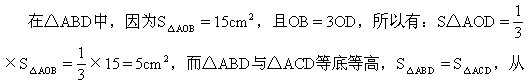
说明答案该是

而S△CDO=15cm2，在△BCD中，因OB=3OD，S△BCO=S△CDO×3=3×15=45cm2，所以梯形ABCD面积=15+5+15+45=80cm2.

5.（35天）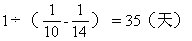

6.（46）

①“3”在个位时，必定是奇数且每十个数中出现一个。1×〔（301-1）÷10〕=30（个）；

②“3”在十位上时，个位数只能是1，3，5，7，9，这个数是奇数。每100个数共有五个。5×［（301-1）÷100］=15（个）；

③“3”在百位上，只有300与301两个数，其中301是奇数。

因此，在1～301所有奇数中，数字“3”出现30+15+1=46（次）。

7.（11天）

（26500-2180×5）÷（2180+420）+5=（26500-10900）÷2600+5=11（天）

8.（76千米/时，120米）

把火车与人的速度差分成8段，火车与汽车速度差也就是1段。可得每段表示的是（67-4）÷（8-1）=9（千米/时）。火车的速度是67+9=76（千米/时），9×1000÷3600=2.5（米/秒），2.5×48=120（米）。

9.（28）

10.(49)

由相向行程问题，若它们一直保持相向爬行，直至相遇所需时间是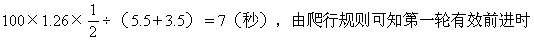

间是1秒，第二轮有效前进时间是5-3=2（秒）……由上表可知实际耗时为1+8+16+24=49（秒），相遇有效时间为1+2×3=7秒。因此，它们相遇时爬行的时间是49秒。

二、解答题：

1. （90岁）

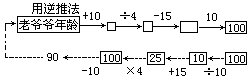
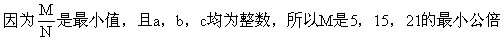
小公倍数；N是28，56，20的最大公约数。因此，符合条件的最小分数：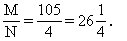

3.（0）

由已知条件得：3a=b+d+e，3b=a+c+f，3c=b+d+g，3d=a+c+h，把这四式相加得3（a+b+c+d）=2（a+b+c+d）+（e+f+g+h）。所以（a+b+c+d）=e+f+g+h，即原式值为0.

4.（1）2厘米

从图中可看出，有（20-1=）19个间隔，每个间隔距离是（44-6）÷19=2（厘米）。

（2）观察三个三角形的迭合。画横行的两个三角形重迭，画井线是三个三角形重迭部分，它是与原来的三角形一般模样，但底边是原来三角形底

×2=3（cm2）。每三个连着的三角形重迭产生这样的一个小三角形，每增加一个大三角形，就多产生个一个三次重迭的三角形，而且与前一个不重迭。因此这样的小三角形共有20-2=18（个），面积之和是3×18=54（cm2）。

（3）

每两个连着的三角形重迭部分，也是原来的三角形一般模样的三角形，

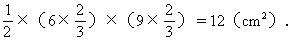
每增加一个大三角形就产生一个小三角形。共产生20-1=19（个），面积19×12=228（cm2）。

所求面积228-54×2=120（cm2）

（4）（312cm2）

20个三角形面积之和，减去重迭部分，其中120cm2重迭一次，54cm2重迭两次。