小学数学奥林匹克模拟试卷（13）

一、填空题：

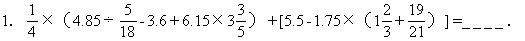
2.已知A=2×3×3×3×3×5×5×7，在A的两位数的因数中，最大的是______.

3.在图中所示的方格中适当地填上1、2、3、4、5、6、7、8，使它的和为153.此时所有“个位数字”之和与所有“十位数字”之和相差_______.

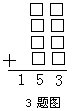
4.A、B两只青蛙玩跳跃游戏，A每次跳10厘米，B每次跳15厘米，它们每秒都只跳1次，且一起从起点开始。在比赛途中，每隔12厘米有一陷阱，当它们中第一只掉进陷阱时，另一只距离最近的陷阱有______厘米。

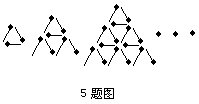
5.如图所示，按一定规律用火柴棍摆放图案：一层的图案用火柴棍2支，二层的图案用火柴棍7支，三层的图案用火柴棍15支，……，二十层的图案用火柴棍______支。

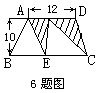
6.图中ABCD是梯形，AECD是平行四边形，则阴影部分的面积是______平方厘米（图中单位：厘米）。

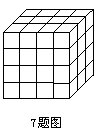
7.用43个边长1厘米的白色小正方体和21个边长1厘米的黑色小正方体堆成如图所示的大正方体，使黑色的面向外露的面积要尽量大。那么这个立方体的表面积上有______平方厘米是黑色的。

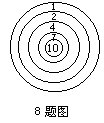
8.甲、乙、丙三人射击，每人打5发子弹，中靶的位置在图中用点表示。计算成绩时发现三人得分相同。

甲说：“我头两发共打了8环。”

乙说：“我头两发共打了9环。”

那么唯一的10环是______打的。

9.有三堆棋子，每堆棋子一样多，并且都有黑白两色棋子。第一堆里黑棋子和第二堆里白棋子的数目相等，第三堆里的黑棋_______分之_______.

10.若干名战士排成八列长方形队列，若增加120人或减少120人都能组成一个新的正方形队列。那么，原有战士_______名。

二、解答题：

1.计算：

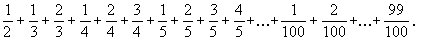
2.甲有桌子若干张，乙有椅子若干把，如果乙用全部椅子换回数量同样多的桌子，则乙需补给甲320元，如乙不补钱，就要少换回5张桌子。已知3张桌子比5把椅子的价钱少48元，那么乙原有椅子多少把？

3.有30个贰分硬币和8个伍分硬币，用这些硬币不能构成1分到1元之间的币值有多少种？

4.快、中、慢三辆车同时从A地沿同一公路开往B地，途中有一骑车人也同方向行进。这三辆车分别用7分、8分、14分追上骑车人。已知快车每分行800米，慢车每分行600米，求中速车的速度。

参考答案：

一、填空题：

1.10

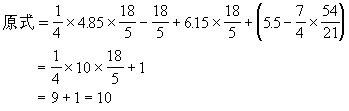
2.90

2×32×5=90

3.10

所有“个位数字”之和=23，所有“十位数字”之和=13，所以23-13=10.

4.4

10与12的最小公倍数是60，15和12的最小公倍数也是60.当第一只掉进陷阱时，第二只跳到10×（60÷15）=40厘米处，此时距离最近的陷阱有40-12×3=4（厘米）。

第一层：1×2

第二层：1×2+1+2×2

第三层：1×2+1+2×2+2+3×2

第二十层：1×2+1+2×2+2+3×2+…+19+20×2

=（1+2+…+19）+1×2+2×2+…+20×2

=190+21×20

=610

6.60

阴影部分的面积等于以12为底以10为高的平行四边形面积的一半，即12×10÷2=60（平方厘米）。

7.50

八个顶点用去8个黑色小立方体，还剩13个黑色小立方体放在棱上，所以大立方体上黑色的面积为

3×8+2×（21-8）=24+26=50（平方厘米）

8.丙。

从图中可以看出，总环数为1×2+2×6+4×3+7×3+10×1=57（环），每人五发子弹打（57÷3=）19环。

从图中还可看出2+6+3+3+1=15，即每人五发子弹均中靶。

因为甲、乙头两发子弹总成绩已分别为8环、9环，所以后三发中不可能有10环，否则总成绩将大于19环。

由此可知，10环是丙打的。

根据条件可知，第一、二堆中，白色棋子与黑色棋子数目相同，所以第一、二堆中的白棋子也可分成同样的3份，因为三堆棋子数相同，所以每堆棋子数相当于3份。

根据第三堆中黑棋子占2份，可知第三堆中白棋子占1份。

因为增加120人可构成大正方形（设边长为a），减少120人可构成小正方形（设边长为b），所以大、小正方形的面积差为240.

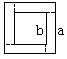
利用弦图求大、小正方形的边长（只求其中一个即可），如右图所示，可知每个小长方形的面积为（240÷4）=60.

根据60=2×30=3×20=4×15=5×12=6×10，试验。

①长=30，宽=2，则b=30-2=28.

原有人数=28×28+120=904（人），经检验是8的倍数（原有8列纵队），满足条件。

②长=20，宽=3，则b=20-3=17.

原有人数为奇数，不能排成8列纵队，舍。

③长=15，宽=4，则b=15-4=11.

原有人数为奇数，不能排成8列纵队，舍。

④长=12，宽=5，则b=12-5=7.

原有人数为奇数，不能排成8列纵队，舍。

⑤长=10，宽=6，则b=10-6=4.

原有人数=4×4+120=136（人）。经检验是8的倍数。满足条件。

所以原有战士904人或136人。

二、解答题

1.

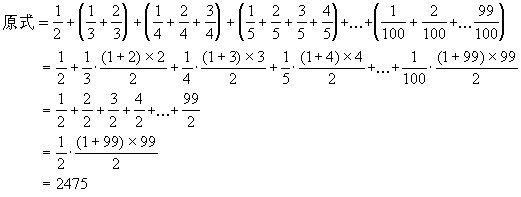
2.20把。

（1）每张桌子多少元？

320÷5=64（元）

（2）每把椅子多少元？

（64×3+48）÷5=48（元）

（3）乙原有椅子多少把？

320÷（64-48）=20（把）

3.4种。

共有人民币：2×30+5×8=100（分）=1（元）。

按如下方法分组，使每组中的币值和为1元：（0，100），（1，99），（2，98），（3，97），…（49，51），（50，50）

因为0，2，4，6，…，50这26个数能用所给硬币构成，所以对应的100，98，96，94，…50也能用所给硬币构成。

下面讨论奇数：1，3，5，7，…，99.

因为4，6，8，10，…，50均可由贰分硬币构成，所以将其中两个贰分币换成一个伍分币，得到5，7，9，11，…，51，可用所给硬币构成。

只有1、3不能构成，对应的99、97也不能构成，所以共有4种不能构成的币值。

4.每分750米。

（1）7分时慢车与快车相距多少米？（800-600）×7=1400（米）

（2）骑车人的速度是每分多少米？600-1400÷（14-7）=400（米）（2）快车出发时与骑车人相距多少米？（800-400）×7=2800（米）

（4）中速车每分行多少米？

400+2800÷8=750（米）