小学数学奥林匹克模拟试卷（15）

一、填空题：

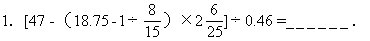
2.筐中有120个苹果，将它们全部都取出来，分成偶数堆，使得每堆的个数相同，有_______种分法。

3.小红上个月做了六次测验，第三、四次的平均分比前两次的平均分多1分，比后两次的平均分少2分。如果后三次平均分比前三次的平均分多3分，那么第四次比第三次多得______分。

原来的______.

5.小明家有若干只小鸡和小兔，已知鸡兔的头数与鸡兔的脚数之比是41∶99，那么小鸡与小兔的只数之比是_______.

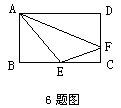
6.如图，已知长方形ABCD的面积是24平方厘米，三角形ABE的面积是5平方厘米，三角形AFD的面积是6平方厘米，那么三角形AEF的面积是______平方厘米。

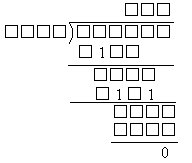
7.下面是一个残缺的算式，所有缺的数字都不是1，那么被除数是______.

8.今年是1997年，父母的年龄（整数）和是78岁，姐弟的年龄（整数）和是17岁，四年后父的年龄是弟的年龄的4倍，母的年龄是姐的年龄的3倍，那么当父的年龄是姐的年龄的3倍时是公元______年。

9.一件工作，甲每天做8小时30天能完成，乙每天做10小时22天就能完成。甲每做6天要休息一天，乙每做5天要休息一天，现两队合做，每天都做8小时，做了13天（包括休息日在内）后，由甲独做，每天做6小时，那么完成这项工作共用了______天。

10.有一串数1，1，2，3，5，8，…，从第三个数起，每个数都是前两个数之和，在这串数的前1997个数中，有______个是5的倍数。

二、解答题：

2.有三块长方形菜地，已知这三个长方形的长相同，第二块比第一块的宽多3米，第三块比第一块的宽少4米，第二块面积是840平方米，第三块面积是630平方米，求第一块地的面积是多少平方米？

3.有6个棱长分别是4厘米、5厘米、6厘米的相同的长方体，把它们的某些面染上红色，使得6个长方体中染有红色的面恰好分别是1个面、2个面、3个面、4个面、5个面和6个面。染色后把所有长方体分割成棱长为1厘米的小正方体，分割完毕后，恰有一面是红色的小正方体最多有多少个？

4.一列长110米的列车，以每小时30千米的速度向北驶去，14点10分火车追上一个向北走的工人，15秒后离开工人，14点16分迎面遇到一个向南走的学生，12秒后离开学生。问工人、学生何时相遇？

参考答案：

一、填空题：

1.

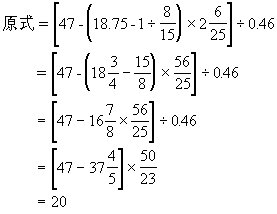
2.

120的偶因数有12个：2，4，6，8，10，12，20，24，30，40，60，120.每个偶因数对应于一种符合条件的分法，所以共有12种分法。

3.3分

根据题设可知：第三、四次的总分比前两次的总分多2分、比后两次的总分少4分，所以后两次的总分比前两次的总分多6分，又根据条件可知，后三次比前三次的总分多9分，所以第四次比第三次多得3分。

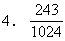
设原有水量为

第一次补完后，有水：

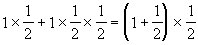
第二次补完后，有水：

……

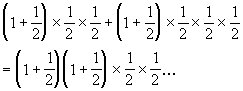
第五次补完后，有水：

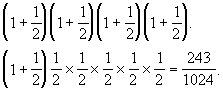
5.65∶

因为平均每41个头有99只脚，即每82个头有198只脚。

假设这82只全是鸡，则应有脚164只。

每增加一只兔子，可增加2只脚，共增加（198-164）÷2=17（只）兔子，此时有鸡（82-17=）65只。

所以鸡与兔的比值是65∶17.

6.9.5平方厘米。

连结长方形对角线AC，可知S△ABC=S△ACD=12（平方厘米）。

因为S△AFD=6（平方厘米），所以S△ACF=6（平方厘米），由此可知F是DC边的中点。

因为S△ABE=5（平方厘米），所以S△AEC=7（平方厘米），由此可知BE∶EC=5∶7.

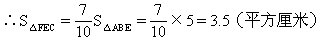
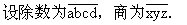
S△AEF=24-5-3.5-6=9.5（平方厘米）。

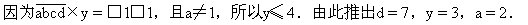
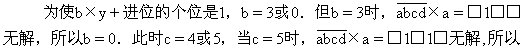
，此时可知x=4.

因为2047×z=□□□□，□中没有1，所以z=2.

故被除数为2047×432=884304.

8.2002年

因为四年后，姐弟年龄之和是25岁，父母年龄之和是86岁。所以此时姐的年龄为

（25×4-86）÷（4-3）=14（岁）

父的年龄是所以今年姐10岁，父40岁，根据

（40-10）÷（3-1）=15（岁）

可知，姐15岁时，父是姐年龄的3倍。因此还要过（15-10=）5年。所以1997+5=2002（年）。

9.23天

一件工作，甲需（8×30=）240小时完成，乙需（10×22=）220小时完成。

所以完成这件工作共用了（13+8+2=）23天。（甲独做时还要再休息两天。）

10.

设这串数中任一个数为a，它的前两个数为b和c，则a=b+c.于是a除以5的余数等于

（b+c）除以5的余数。

再设b=5m+r1，c=5n+r2，所以

a=（5m+r1）+（5n+r2）

=5（m+n）+（r1+r2）由此可知，a除以5的余数等于（r1+r2）除以5的余数，即等于前两个数除以5的余数之和再除以5的余数。

所以这串数除以5的余数分别为：

1，1，2，3，0，3，3，1，4，0，4，4，3，2，0，2，2，4，1，0，1，1，2，3，0，……可以发现，这串余数中，每20个数为一个循环，且一个循环中，每5个数中第一个是5的倍数。

1997÷5=399…

所以前1997个数中，有399个是5的倍数。

二、解答题：

1.1

……

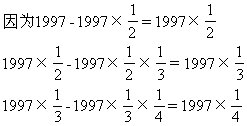
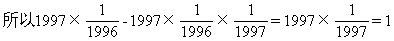
2.750平方米

根据题设可知，第三块比第二块的宽多（4＋3=）7米，所以每块长方形的长为

（840-630）÷（4+3）=30（米）

第一块地的面积为：

30×（630÷30＋4）=750（米）

3.318个

一面染色时，最多可得到（5×6=）30个一面是红色的小正方体。

二面染色时，最多可得到（30×2=）60个一面是红色的小正方体。

三面染色时，最多可得到（60＋5×2-5×2=）60个一面是红色的小正方体。

四面染色时，最多可得到（60＋5×2-5×2=）60个一面是红色的小正方体。

五面染色时，最多可得到（60＋8-12=）56个一面是红色的小正方体。

六面染色时，最多可得到（56＋8-12=）52个一面是红色的小正方体。

所以共有一面是红色的小正方体。

30＋60+60+60+56＋52=318（个）

4.14点40分

（1）火车的速度是每秒多少米？

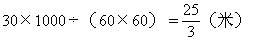
（2）工人的速度是每秒多少米？

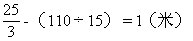
（3）学生的速度是每秒多少米？

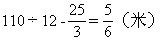
（4）14点16分时学生、工人相距多远？

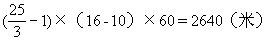
（5）学生、工人相遇需要多少分？

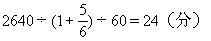
（6）学生、工人相遇时间：

14点16分+24分=14点40分