小学数学奥林匹克模拟试卷（18）

一、填空题：

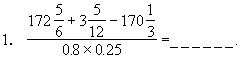
2.将1997加上一个整数，使和能被23与31整除，加的整数要尽可能小，那么所加的整数是______.

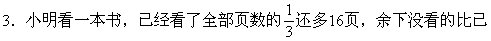看过的还多48页，这本书共有______页。

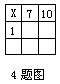
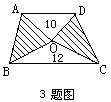
4.如图，每一横行、每一竖行和对角线上三个数之和均相等，则x=______.

5.下面的字母算式中，每一个字母代表一个数字，不同的字母代表不同的数字。如果CHINA代表的五位数能被24整除，那么这个五位数是______.

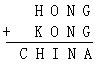
6.有四个数，每次选取其中两个数，算出它们的和，再减去另外两个数的平均数，用这种方法计算了六次，分别得到以下六个数：43、51、57、63、69、78.那么原来四个数的平均数是_______.

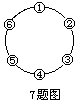
7.有一枚棋子放在图中的1号位置上，现按顺时针方向，第一次跳一步，跳到2号位置；第二次跳两步，跳到4号位置；第三次跳三步，又跳到1号位置；……，这样一直进行下去，______号位置永远跳不到。

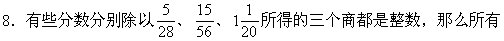这样的分数中最小的一个是______.

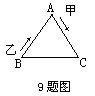
9.如图，等边三角形ABC的边长为100米，甲自A点，乙自B点同时出发，按顺时针方向沿着三角形的边行进。甲每分钟走60米，乙每分钟走90米，在过每个顶点时各人都因转弯而耽误10秒钟，那么乙在出发______秒之后追上甲。

10.把一个大长方体木块表面上涂满红色后，分割成若干个同样大小的小长方体，其中只有两个面是红色的小长方体恰好是12块，那么至少要把这个大长方体分割成_______个小长方体。

二、解答题：

1.计算：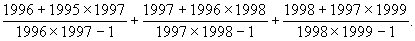

2.一件工作，甲独做要8小时完成，乙独做要12小时完成。如果先由甲工作1小时，然后由乙接替甲工作1小时，再由甲接替乙工作1小时，……，两人如此交替工作那么完成任务时共用了多少小时？

3.如图，在一个梯形内有两个三角形的面积分别为10和12，已知梯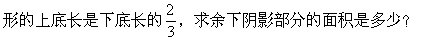

4.一个自然数除以6得到的商加上这个数除以7的余数，其和是11，求所有满足条件的自然数。

参考答案:

一、填空题：

2.142

因为1997与所求整数之和是23与31的公倍数，所以有

23×

713×

142为所加整数。

3.240

16＋48+16=80（页）

所以这本书共有

4.22

为方便起见，原图中的空格用字母表示，如图所示。

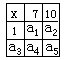
可以看出，每一横行、每一竖行及对角线上的三个数之和为（x＋7＋10=）x＋17

显然a3=17＋x-x-1=16

a1=17+x-10-16=x-9

a2=17＋x-（x-9）-1＝25

a5=17+x-10-25=x-18

所以x＋（x-9）＋（x-18）=x+17

2x＝44

x=22

5.17208

显然C=1，K=9，且百位向千位进1.

因为在十位上，N=9（个位向十位进1），或N=0，由于K=9，所以N=0.

在百位上，由于百位向千位进1，所以O=5，6，7，8.试验：

若O=5，则I=0，与N=0重复。

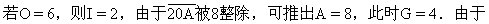
＋2＋0＋8=11，所以H=7（1，4已被取过）。

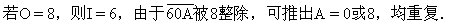
所以五位数是17208.

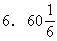
因为在四个数中每次选取两个数求和，计算六次，等于每个数计算了三次，即四数之和的3倍。每次计算两个数的平均数，计算六次，等于四数之

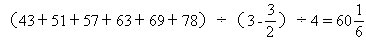
7.3号、6号

经试验可以发现，棋子每次跳到的位置依次是2、4、1、5、4、4、5、1、4、2、1、1、2、4、1、…每12次为一个循环，所以3、6号位置永远跳不到。

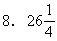
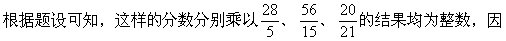
此分数的分子应是5、15、21的公倍数，分母是28、56、20的公约数。为使这样的分数取最小，则分子是5、15、21的最小公倍数为105，分母是

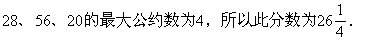
9.250

V甲=60米/分=1米/秒，V乙=90米/分=1.5米/秒。根据题意可知，乙为追上甲，需要多走100米还要多转一个转弯，但在转弯处还要耽误10秒钟，此时甲又多走出10米，所以甲、乙的距离差为（100＋10=）110米，乙追上甲时共行了

1.5×110÷（1.5-1）=330（米）

由此可知，乙需拐三次弯，需要30秒，所以乙追上甲时共需时间

110÷（1.5-1）＋30=250（秒）

10.20

因为只有两个面是红色的小长方体位于棱上（除去棱的端点），为使分割的块数尽量少，可使12条棱中有8条棱只有端点的两个小长方体，另外4条棱的中间分别有（12÷4=）3个小长方体，所以共分割成小长方体的个数为

（3＋2）×2×2=20（个）

二、解答题：

1.3

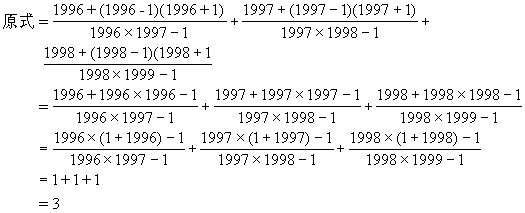
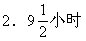
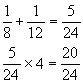
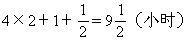
3.23

设上底长为2a，下底长为3a，三角形AOD的高为h，则三角形BCO的高为

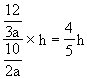
因为三角形AOD面积为10，可知

ah＝10

所以梯形面积为

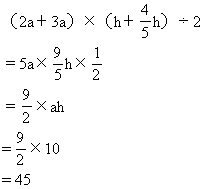
故阴影面积为

45-（10＋12）

4.（34，40，46，52，58，64，70）

一个数除以7的余数有7种可能：6，5，4，3，2，1，0.

若余数为6，则这个数除以6的商为（11-6=）5，这个数在30～36之间，此区间中只有34被7除余6.

若余数为5，则这个数除以6的商为（11-5=）6，这个数在36～42之间，此区间中只有40被7除余5.

依此类推，可以得到相应的其余几个数：46，