初中数学有理数混合运算解题指导

有理数的混合运算是《有理数及其运算》一章的重点，也是初中继续学习数学的基础。因此，熟练地进行有理数混合运算是至关重要的，但同学们在具体的集体过程中往往因为马虎而丢分。

因为马虎而丢分，同学们会感觉很委屈，我明明会做啊！我们如何在平时的学习中将有理数运算中的“虾兵蟹将”全部拿下？于老师根据近几年的教学经验，以及目前初一孩子的学习习惯，给同学们提几点建议：

一、牢记各种运算法则

有理数的混合运算说穿了就是有理数的加、减、乘、除和乘方这五种运算的组合，无论什么样的混合运算，最终都要化归为这五种运算，因此，牢记这五种运算的法则在运算中对号入座是进行混合运算的前提。大家可能会说，加、减、乘、除运算其实我小学都学习过，乘方也简单接触过，小学时我基本上都是全对，为什么到初中就总是错呢？

提出这样一问的同学可能忽略了一个问题。我们初中所学的有理数，重要的是引进了负数，大家回想一下，我们多少错误的罪魁祸首是正负号？从正负号上延伸出来的数轴、相反数、绝对值、（负）倒数等概念也在阻挠我们的视线！因此，要想拿下有理数混合运算全部的“虾兵蟹将”就要对负数理解透彻，同时切实理解数轴、相反数、绝对值、（负）倒数等概念，计算关键是符号，不要搞错。大家请这道题：（2011—2012年七年级上学期期末测试题，16题）。

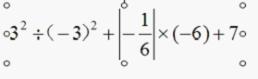
大家一看，说这道题很简单，但是仍然有很多同学做错，错误常常出现在：1、知道-3的平方是9，但是当计算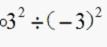时就稀里糊涂的得-1； 2、做题时，嘴里时时念着“负负得正”没看清绝对值号；结果可想而知，煮熟的鸭子飞了，这分丢的是在可惜！

二、严格遵循运算顺序

无规矩难以成方圆.在混合运算中，一定要严格按照运算顺序的规定进行，否则相同的题目将出现五花八门的不同答案。关于运算顺序，要注意以下四点：

1.若算式中不含括号，而含三级运算，则从高级到低级依次进行；即先算三级运算(乘方)，再算二级运算(乘、除)，最后算一级运算(加、减).如计算：3×(-2)3+2，先算乘方(-2)3=-8，再算乘法3×(-8)=-24，最后算加法-24+2=-22，即原式=3×(-8)+2=-24+2=-22.

2.若算式中只含加、减或乘、除，即同级运算，则运算顺序要从左到右依次进行.如计算：18÷(-6)÷3，应先算18÷(-6)=-3，再算-3÷3=-1；切忌先算(-6)÷3=-2，再算18÷(-2)=-9.

3.若算式含有括号，则先做括号里的运算，而括号里的运算顺序同样按上述的两点进行.

4.若算式中含有多种运算，则可按加、减、乘、除分段同时进行计算.如计算：(-3)×(-6)÷(-3)2-(-15)÷5，在计算乘方(-3)2的同时还可以计算(-3)×(-6)与(-15)÷5，即原式=18÷9-(-3)=2+3=5.

三、合理运用运算律

合理运用运算律是提高有理数运算能力的基本保证，在运用时，一定要分清各种运算律的名称和使用的方法及条件。

1.加法交换律和结合律通常在加、减运算中同时使用，交换的目的在于结合，结合时一般是按相反数结合、按可以凑整的结合、按分母相同的结合、按正负结合，总之，将容易计算的数进行结合。

2.乘法交换律和结合律通常在乘、除运算中使用，交换的目的同样是为了结合，结合时一般将能约分的数结合。

3.分配律是乘法对加法的分配，它既可以正用(即a(b+c)=ab+ac)，也可以逆用(即ab+ac=a(b+c))，切记：除法没有分配率！！！！不要出现12÷(4+3)=12÷4+12÷3=3+4=7的错误。

4.含多重括号时，要注意灵活去括号，没必要墨守成规，总是先去小括号，再去中括号，最后去大括号。在去括号时要牢记“括号前面是负号时，括号内各项均要变号。”很多同学在遇到这类问题是，若括号内有多项时，前两个知道变号，后面的就忘了，接下来，悲剧就发生了······

四、不可原谅的低级错误

有些同学会犯一些不可原谅的错误：

1、因为书写潦草，3和5不分，5和8不分，1和7不分，绝对值号书写不规范，第二步自己看成是小括号，等等其他五花八门的错误。

2、从上往下抄错，掉个负号，漏掉一项等等。

3、解题格式问题：老师在课堂上反复强调的解题格式“解：原式=”，可一到考场上，扔有不少同学忘记写。那么付出的代价就是这道题虽然做对了，结果还是少得一分！

以上信息由论坛名师进行整理，感谢于老师的分享。

以上指导，希望对郑州新初一的同学们有帮助。小编提醒，初一阶段，同学们要养成主动学习的好习惯。