小升初奥数天天练数论——完全平方数综合
题目：有4个不同的数字共可组成18个不同的4位数．将这18个不同的4位数由小到大排成一排，其中第一个是一个完全平方数，倒数第二个也是完全平方数．那么这18个数的平均数是： ．
答案：一般而言，4个不同的数字共可组成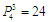
（个）不同的4位数．如果只能组成18个不同的4位数，说明其中必有0，即按
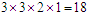算出来的．在这四个不同的数中，则设最小的数
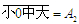，倒数第二个则是
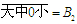，两数正好是一对反序数．根据完全平方数特点，小、大两数必是1，4，6，9之中的两个．且中数在小大之间．
可以为以下3类：
当大=4，在1024、1034中，1034不是完全平方数，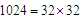
，但4201不成立．
当大=6，1026、1036、1046、1056、4056．都不是完全平方数．
当大＝9，
在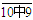
的数中，取
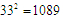，而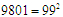
在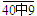
的数中，取632，672不成立．
在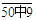
的数中，取672，732不成立．
在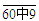
的数中，取732，772不成立．
所以，符合条件的数只能是由1089开始的四位数，
求这18个数的和，有两种方法，一种是枚举法，另一种是概率法，可以作为方法来记：
即，对于没有0的四位数a，b，c，d排列互不相同的四位数时，共有24个数，每个数字在每位上出现的概率机会是一样的，所以，每个数字在每位上都出现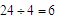
（次）．
则总和为：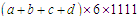
．
如果有一个数是0，则在此基础上，考虑0作首位的部分要排除．
即：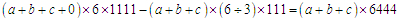
，
所以，本题的总和为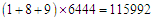
，所以，这18个数的平均数为
．
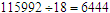分析：此题为2008年数学解题能力展示初赛试题，考查了完全平方数、计数、平均数的综合，难度较大，而且计算时还包含了一些技巧，所以当年考试正确率比较低。此题综合性比较强，所以对学生而言难度也就比较大，如果非常熟悉平均数，是可以跳过前面复杂的分类讨论阶段，直接试数2~3次即可得到1、0、8、9这几个数字，然后求得平均数即可。但是对于不熟悉平方数的学生，此题会浪费很多时间。