小升初奥数天天练数论——试除法
2014-02-25 18:09:11
标签：小升初奥数天天练
考点：试除法
难度：3星
来源：思维导引
题目：在六位数11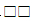
11中的两个方框内各填入一个数字，使此数能被17和19整除，那么方框中的两位数是多少?
答案：采用试除法.设六位数为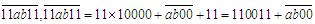
如果一个数能同时被17和19整除，那么一定能被323整除．
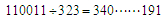，余191也可以看成不足323-191=132．所以当
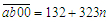时，即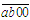
是100的倍数时，六位数才是323的倍数．所以有323n的末位只能是10-2=8，所以n只能是6，16，26， 验证有n=16时，
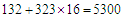，所以原题的方框中填入5，3得到的115311满足题意．
分析：试除法是整除问题中非常重要的方法，可以用于对未知结果的直接试除，但是同时对数字的使用也有一定要求，如果只是限定在某几个数字中使用，试除法会受到较大的限制。一般对不常见的数，或者没有掌握整除特点的数，或者很多数同时需要整除时，都可以用试除法来解决。
查看全部
来源：查字典小升初网