培养发散性思维的几道题

如图，$RtvartriangleABC$中$angleC=90^circ$，以斜边$AB$为边向外作正方形$ABDE$，且正方形对角线交于点$O$，连接$OC$，已知$AC=5$，$OC=6sqrt{2}$，则另一直角边$BC$的长为__________.

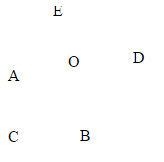
解法一：如图1所示，过$O$作$OFbotBC$，过$A$作$AMbotOF$，

$because$四边形$ABDE$为正方形，

$therefore$$angleAOB=90^circ$，$OA=OB$，

$therefore$$angleAOM+angleBOF=90^{circ}$，

又$angleAMO=90^{circ}$，$therefore$$angleAOF+angleOAM=90^{circ}$，

$therefore$$angleBOF=angleOAM$，

在$vartriangleAOM$和$vartriangleBOF$中，

$left{begin{array}{}{l}{angleAMC=angleOFB=90^circ}\{angleOAM=angleBOF}\{OA=OB}\end{array}right.$，

$therefore$$vartriangleAOMcongvartriangleBOF(AAS)$，

$therefore$$begin{array}{}{l}{AM=OF}\end{array}$，$OM=FB$，

又$angleACB=angleAMF=angleCFM=90^{circ}$，

$therefore$四边形$ACFM$为矩形，

∴$AM=CF$，$AC=MF=5$，

$therefore$$OF=CF$，

$therefore$$vartriangleOCF$为等腰直角三角形，

∵$OC=6sqrt{2}$，

$therefore$根据勾股定理得：$CF^{2}+OF^{2}=OC^{2}$，

解得：$CF=OF=6$，

$therefore$$FB=OM=OF-FM=6-5=1$，

则$BC=BF+CF=6+1=7$.

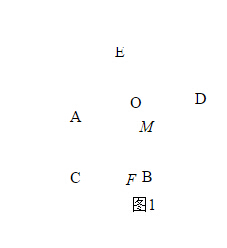
解法二：如图2所示，过点$O$作$OMbotCA$，交$CA$的延长线于点$M$;过点$O$作$ONbotBC$于点$N$.

易证$DeltaOMAcongDeltaONB(AAS)$，$thereforeOM=ON,MA=NB$,

$thereforeO$点在$angleACB$的平分线上，$thereforeOCM$为等腰直角三角形，

又$OC=6sqrt{2}$，$thereforeCM=6,thereforeMA=CM-AC=6-5=1$,

$thereforeBC=CN+NB=6+1=7$