透析杯赛“中点相遇”及“两次相遇”命题原理和解题技巧
查字典武汉奥数网11月14日:本文通过举一反三,透析小升初奥数杯赛考试中的行程问题——“中点相遇”及“两次相遇”命题原理和解题技巧!
第一篇:【透析杯赛“中点相遇”命题原理和解题技巧】
是指在距离中点的某个地方相遇。借助中点,可以帮我们找到两人的路程差(即‘多走的路程’是相遇地点距离中点路程的2倍),再结合速度差,可以求出相遇时间和总路程。解题时,关键要把握两种情形:同时出发和不同时出发。下面我们以几个典型试题为例进行具体分析和拓展,以便同学们熟练掌握这种题型的命题特点和答题技巧。
【举一】
小花猫和小花狗是一对好朋友,它们分别从A、B两地同时出发,相向而行,小花猫每分钟行80米,小花狗每分钟行100米,它们在途中的C处相遇。问:A、B两地之间的距离是多少米?
考点透析:围绕中点找两人的路程差。由于小花猫先走9分钟,走了80×9=720米,结果小花猫先过中点。解题核心是找出猫和狗在‘相遇时间’内的路程差。相遇时,小花猫比小花狗多走280×2=560米,这560米是小花猫提前9分钟的结果,但为什么不是720米呢?即9分钟后,小花狗在‘相遇时间’内又追回了80×9-560=160米,进而可知‘相遇时间’是160÷(100-80)=8分钟。
解答:280×2=560(米)
80×9-560=160(米)
160÷(100-80)=8(分)
80×9+(80+100)×8=2160(米)
答:略。
【反三】
1、甲、乙两人同时从两地相向跑步而行,甲每小时行12千米,乙每小时行10千米,两人刚好在距中点3千米处相遇,问两地相距多少千米?
考点透析: 同时出发,则相遇时间就是走完全程的时间。路程差是相遇点距离中点的2倍,2×3=6千米,再根据甲乙的速度差可以求出相遇时间。
解答:3×2=6(千米)
6÷(12-10)=3(小时)
3×(12+10)=66(千米)
答:略。

2013创新杯高频考点解析:行程模块
2013创新杯高频考点解析:数论组合
透析小学奥数杯赛中的图形问题
透析杯赛“中点相遇”及“两次相遇”命题原理和解题技巧
如何推翻数学竞赛中的四座大山:数、行、形、算
武汉市小升初奥数杯赛介绍及影响力
新希望杯报名:千万不要去牛娃扎堆的机构报名
2、甲、乙二人从A,B两地同时出发相向而行,甲每分钟行80米,乙每分钟行70米,出发一段时间后,二人在距中点60米处相遇。如果甲晚出发一会儿,那么二人在距中点220米处相遇。甲晚出发了多少分钟?
考点透析: 甲晚出发的时间=乙第二次需要的时间-甲第二次需要的时间。题目中有两个与中点相关的路程,根据第一次相遇地点与中点比较,可以求出总路程;根据第二次相遇地点与中点比较,可以求出第二次相遇后,甲、乙各自行走的路程和时间。
解答:60×2÷(80-70)=12(分)
12×(80+70)=1800(米)
(1800÷2+220)÷70=16(分)
(1800÷2-220)÷80=8.5(分)
16-8.5=7.5(分)
答:略。
3、在一个边长为17米的正方形ABCD的A点,有红、蓝两个甲虫从9点开始,同时沿着边以相同的速度爬行。红甲虫由A-B-C-D,蓝甲虫由A-D-C,9:30红甲虫爬到AB间距A点10 米的E点后继续向前爬行,10:15爬到BC间的F点,再经过C向前爬去,蓝甲虫爬到AD间距D点5米的G点,休息一会再往前爬行。当两个甲虫在CD上H点相遇时,凑巧四边形EFHG的面积是正方形面积的一半,问蓝甲虫在G点休息了多长时间?
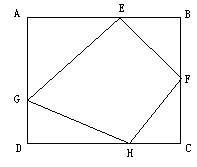
考点透析: 这个题目的核心是考察中点相遇。两虫速度相同,如同时出发,中途不休息,两虫会同时到达C点(即中点),但是如果有一方休息,那么另一方就会超过中点与其相遇,‘多走的路程’所需的时间即为休息时间。
解答:设DH为x,则HC=17-x,因为四边形EFGH的面积是正方形面积的一半,所以图形中四个三角形的面积和为正方形面积的一半。则有:
10×12÷2+7×8÷2+5x÷2+9(17-x)÷2=17×17÷2
x=10
相遇地点距离中点的路程:17-10=7(米)
红甲虫比蓝甲虫多走了:7×2=14(米)
因为爬行10米要30分钟,所以爬行14米要30÷10×14=42(分),所以蓝甲虫休息了42分钟。
答:略。
第二篇:【透析两次相遇的命题原理和解题技巧】
“ 两次相遇”问题,是指出发后相遇两次,通常根据两次相遇地点与某个地方的距离可以求出两地之间的路程,或由此衍生出来的其它问题。这是相遇问题中一种非常典型的题型,是升学、择校、竞赛等检测中的常考知识。解决两次相遇问题,关键是把握两次相遇合走多个全程,以及每个物体各走的路程与全程的关系,同时灵活应对“同时与不同时”、“同地与不同地”、“同向与不同向”出发的特点。以下是两次相遇合走三个全程与四个全程的情况,供大家了解:
【举一】
甲、乙两辆汽车同时从A、B两地相对开出,在距A侧60千米处第一次相遇,相遇以后,两车继续前进,到达对方出发站后又立即返回,在距B侧40千米处第二次相遇。求A、B之间的路程?如果两车继续前进,则在何处第三次迎面相遇?
考点透析: 如图若只看甲的轨迹,可以发现,第二次相遇时,甲走了一个全程多40千米;第一次相遇时,甲走了60千米,说明甲乙每合走一个全程,甲都会行60千米。第二次相遇,甲乙合走三个全程,则甲走3个60千米,即180千米,那么一个全程是180—40=140千米.若继续前进,三次相遇合走五个全程,进而可知第三次相遇的位置即甲现在的位置.
解:(1)60×3—40=140(千米)
(2)60×5=300(千米)
300—140×2=20(千米)距离A侧20千米处
或者140—20=120(千米)距离B侧120千米处
答:略.
【反三】
1、甲、乙两辆汽车分别以不同的速度从A、B两城相对而行,途中相遇,相遇点距A城80千米,相遇后两车继续以原速前进,到达对方出发地后,两车立即返回,在途中第二次相遇,这时相遇点距A城50千米。求A、B两城相距多少千米?如果两车继续前进,则在何处第三次迎面相遇?
考点透析:两次相遇共走三个全程.因而甲共走了3个80千米,即240千米。但第二次相遇的位置是距离A城50千米,而不是距离B城,有什么区别?如果甲车继续向前走50千米回到A城的话(如图),它走的路程正好是一去一返两个全程,从而知道AB的距离.若继续前进,到第三次相遇时,两车还需要走完两个全程,甲应再走2×80=160千米,甲不仅可以回到A城,还可以再走160—50=110千米.
解:(1)80×3+50=290(千米)
290÷2=145(千米)
(2)2×80=160(千米)
160—50=110(千米)距离A城110千米处
或者145—110=35(千米)距离B城35千米处
答:略.
2、甲、乙两辆汽车从AB两地同时相向而行,第一次相遇时甲走了75千米,相遇后两车继续以原速行驶,分别到达BA后,立即返回,在距中点B侧15千米处再次相遇。AB两地相距多少千米?
考点透析:两次相遇共走三个全程.而问题的关键是,若甲第二次相遇后,再走15千米,则甲走的路程正好相当于一个半全程!(思考:如果是距离A侧15千米呢,你会吗?)
解:75×3+15=240(千米)
240÷(1+0.5)=160(千米)
答:略.
3、甲、乙两辆汽车同时从A城出发,并在A城和B城之间往返行驶,甲的速度是70千米/时,比乙的速度更快,两车第一次相遇时距离A城100千米,第二次相遇时距离A城40千米,请问从出发到第二次相遇需要几小时?
考点透析:这里的两次相遇,还是三个全程吗?注意是从同一地出发,即同向而行。因而第一次相遇,必定是速度快的甲先到达B城,然后再调头与乙相遇,所以两车共走了两个全程,此时距离A城100千米,说明在两个全程中乙车只走了100千米.那么第二次相遇时,两车共走了四个全程,乙车应走2个100千米,即200千米,如果乙车继续向前走40千米的话(如图),则它走的路程就是两个全程,一个全程是(200+40)÷2=120千米.那四个全程的和,以及甲共走的路程分别是多少呢?再用甲走的路程除以甲的速度,就是出发到第二次相遇的时间.
解:(100×2+40)÷2=120(千米)
120×4=480(千米)
480—200=280(千米)
280÷70=4(小时)
答:略.

2013创新杯高频考点解析:行程模块
2013创新杯高频考点解析:数论组合
透析小学奥数杯赛中的图形问题
透析杯赛“中点相遇”及“两次相遇”命题原理和解题技巧
如何推翻数学竞赛中的四座大山:数、行、形、算
武汉市小升初奥数杯赛介绍及影响力
新希望杯报名:千万不要去牛娃扎堆的机构报名