数学难题的“耍赖”解法

对正在积极备战“小升初”的六年级同学来说，求阴影部分面积的几何题目自然会成为备考的重点，今天我们就来介绍一种解此类难题的神奇方法——特殊值法，一会儿看两道题你就会发现，原来用这种“耍赖”的方法做题简直妙不可言。

【例1】如图，阴影部分四边形的外接图形是边长为10cm的正方形，则阴影部分的四边形的面积是_____cm2

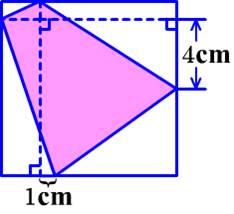
方法一：

【分析】让求阴影部分的面积，怎么算这个阴影部分的面积呢？猛然一看还不会。遇到一道数学难题，如果不会算不要紧，自己画下图，清晰地认识一下图形，看它是怎么画出来的。在这个过程中既是对题目条件的梳理，也是我们接下来分析解题方法的基础。

但是这道题目在画的时候你会发现，四边形的四个顶点你能确定它在哪儿吗？根本就确定不了，也就是说这个题存在图形不确定的问题，这个图谁都确定不了。那谁都确定不了，我也不知道顶点在哪儿，是不是画它在哪儿，它就在哪儿。那怎么画这个题能够特殊一点、好做一点呢？这就可以采取一种思想——特值思想。

【解】因为四边形的顶点位置不确定，可以将顶点进行移动（特殊化成下面的图形，只要顶点之间的相对位置关系不变就可以了！）

自然很容易就能求出，阴影部分的面积等于正方形的面积减去三个直角三角形的面积：

100-（20+5+27）=48（cm2）

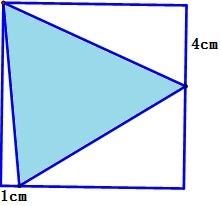
方法二：

【分析】题目中“1cm”和“4cm”这两个条件看似没有关系，解一道题目只有将条件之间建立关系，进行碰撞才能做出来，一道题目单打独斗肯定无法解题，那我就可以做下图所示的辅助线，将“1cm”和“4cm”放在中间的小长方形中。

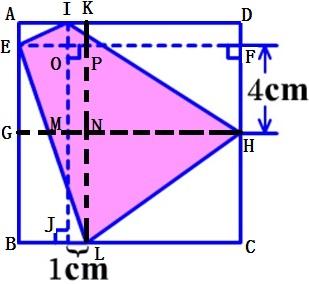
【解】如上图，在长方形AEOI中，阴影部分面积等于空白部分面积；在长方形EBLP中，阴影部分面积等于空白部分面积；在长方形NLCH中，阴影部分面积等于空白部分面积。

则剩下的部分是一个六边形IOPNHDI，六条边分别是IO、OP、PN、NH、HD、DI，在这个图形中，空白部分面积要大于阴影部分面积，并且阴影部分面积加上长方形OMNP的面积等于空白部分面积。

即整个图形中，空白部分面积比阴影部分面积多一个长方形OMNP的面积（即1×4=4cm2）

阴影+空白=100

空白+阴影=4

综上，阴影部分的面积是（100-4）÷2=48（cm2）。

【例二】如图，四边形ABCD面积是1。E、F、G、H分别是四边形的三等分点，即AE＝2EB、HD＝2AH、CG＝2GD、BF＝2CF，那么四边形EFGH的面积是_______。

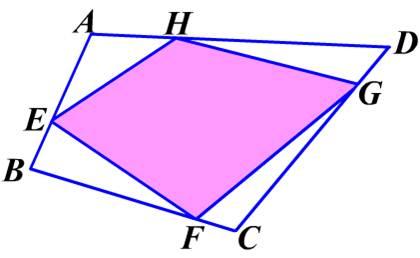
【分析】还是利用上面的阶梯思想：自己画图时发现四边形ABCD的形状根本无法确定，这个时候我们就可以利用“特殊值思想”。

【解】将四边形ABCD变成一个正方形，如下图：

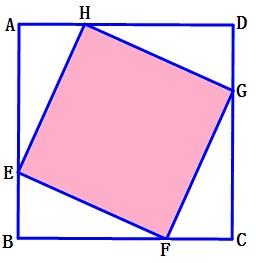
则阴影部分的面积就是整体的面积减去四个直角三角形的面积，因为正方形ABCD的面积是1，则正方形的边长为1，E、F、G、H都是各边的三等分点，那么AH=1/3，AE=2/3，直角三角形AEH的面积就是1/9。

阴影部分面积=1-4/9=5/9。

从上面两道题目来看，遇到这些图形细节无法确定的题目或者“动点问题”时，灵活选取这些“特殊值”法，虽说有些“耍赖”，但是解决问题是有准又快的，尤其是在做一些选择题和填空题时更是如鱼得水。