长沙小升初奥数行程问题之火车过桥知识点

行程问题是应用题里面非常常见和易考的一类题型，e度徐丽老师会针对行程问题中的火车过桥问题进行解析，对于不同题型均会有例题讲解分析以及精选练习题，以供大家有针对性学习巩固，相信大家对于行程问题的攻克将不在话下！

知识点

火车在行驶过程中经常发生过桥与过隧道、两车对开错车和快车超越慢车等情况，所以，火车过桥问题可以分为四种情况：

（1）车与桥

火车过桥是指“全车通过”，即从车头上桥直到车尾离桥才算“过桥”，如下图所示：

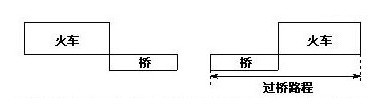
火车过桥的总路程是桥长加车长，这是解决火车过桥问题的关键。火车过桥问题也要用到一般行程问题的基本数量关系：

（2）车与人

火车与人的相遇、追击问题，由于人的宽度跟火车比起来可以忽略不计，所以相关公式我们可以根据行程问题的相遇、追击基本公式变形为：

相遇：路程和=火车车长

速度和=车速+人速

相遇时间=火车车长÷（车速+人速）

追及：路程差=火车车长

速度差=车速－人速

追及时间=火车车长÷（车速－人速）

（3）车与车

火车与火车的相遇、追击问题，由于火车的宽度不可以忽略不计，所以相关公式我们可以根据行程问题的相遇、追击基本公式变形为：

①两列火车相遇情况：

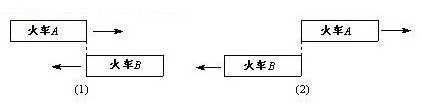
图中（1）表示“碰上”，图中（2）表示“错过”。“碰上”时两列火车车头相遇，“错过”时两列火车车尾离开。

路程和=甲车长+乙车长

速度和=甲车速+乙车速

相遇时间=（甲车长+乙车长）÷（甲车速+乙车速）

②两列火车追击情况：

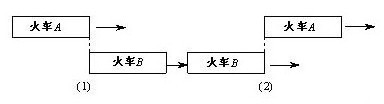
图中（1）表示“追上”，图中（2）表示“超过”。从“追上”到“超过”就是一个追击过程。比较两个火车头，“追上”时A落后B的车身长，“超过”时A领先B的车身长，也就是说，从“追上”到“超过”，A的车头比B的车头多走的路程是：B的车身长+A的车身长。

路程差=快车长+慢车长

速度差=快车速－慢车速

追及时间=（快车长+慢车长）÷（快车速－慢车速）

（4）错车：头对齐，尾对齐

错车问题指的是在直线型道路上同向（相向行驶就是我们上面讨论的两车相遇问题）行驶的两辆列车，它们交错时的速度、时间和车长之间的关系问题。我们分两种情况：

头对齐：路程差=快车车长， 速度差=快车速－慢车速

快车车长÷（快车速－慢车速）=错车时间

尾对齐：路程差=慢车车长， 速度差=快车速－慢车速，

慢车车长÷（快车速－慢车速）=错车时间