[答案]2011.8.18四年级奥数天天练
2011-08-22 16:15:06
标签:小升初真题
难度:★★★★
小学四年级奥数天天练:
100个连续自然数的和是8450取其中第1个,第3个,第5个,…,第99个(所有第奇数个),再把这50个数相加,和是多少?
【分析】 因为100个连续自然数中的所有第奇数个自然数构成了公差为2的等差数列,所以常规的思路是把这50个自然数求出来之后再求和,这是一种从局部到整体的分析策略.(动笔算算看!)
运用对应的思想去分析却别有一番天地.
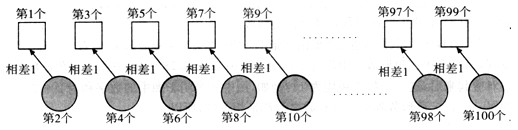
如上图所示,我们虽然不知道这lOO个连续自然数具体是几,但我们可以把这100个连续自然数进行配对:(第1个,第2个)、(第3个,第4个)、…、(第99个,第100个)
配对后,显然每一对自然数相差1.那么所有“第奇数个自然数的和”比所有“第偶数个自然数的和”少50. 由此问题转化为一个和差问题,而所有第奇数个自然数的和(8450—50)÷2=4200.
难度:★★★★★
小学四年级奥数天天练:
从1985到4891的整数中,十位数字与个位数字相同的数共有多少个?
【分析】 根据条件“十位数字与个位数字相同”,所以我们可以设想把相同的两个数“合并”成一个数,这样一来,四位数就变成了三位数.
把在1985~4891的自然数中十位数字与个位数字相同的数1988、1999、…、4888 与“合并”后的三位数建立一一对应关系:

因为上述三位数共有488-198+1=291个,所以,在1985~4891的整数 中,十位数字与个位数字相同的数也有291(个).
查看全部
来源:查字典小升初网