【答案】2011.9.13六年级奥数天天练
2011-09-14 11:23:41
标签：小升初真题
难度：★★★★
【答案】
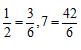，在4，5，…，41这38个数中，有19个是2的倍数，12个是3的倍数，6个6的倍数，因此其中有38-19-12+6=13 个与6互质，即答案为13．
难度：★★★★★
(第四届走美初赛试题)2006盏亮着的电灯，各有一个拉线开关控制，按顺序编号为l，2，…，2006.将编号为2的倍数的灯的拉线各拉一下；再将 编号为3的倍数的灯的拉线各拉一下，最后将编号为5的倍数的灯的拉线各拉一下．拉完后亮着的灯数为__________盏．
【答案】
因为灯在开始的时候是亮着的，所以拉了两次或者没拉的灯最后还是亮的．这道题实际上是求1到2006中不能被2、3、5整除的数和只能同时被2、3、5中2个数整除的数的总个数．
我们可以求得被2整除的数有 2006÷2=1003(盏)，
被3整除的数有 2006÷3=668L2，共668(盏)，
被5整除的数有2006÷5=401L1 ，共401(盏)．
其中，同时被2、3整除的数有2006÷（2×3）=334L2 ，共334(盏)；
同时被3、5整除的有2006÷（3×5）=133L11 ，共133(盏)；
同时被2、5整除的数有2006÷（2×5）=200L6 ，共200(盏)；
同时被2、3、5整除的数有2006÷（2×3×5）=66L26 ，共66(盏)，所以，只能同时被2、3、5中2个数整除的数的个数为 334+133+200-3×66=469(盏)，不能被2、3、5整除的数的个数为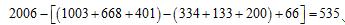 
(盏)．所以，最后亮着的灯一共为469+535=1004 (盏)．
查看全部
来源：查字典小升初网