【答案】2011.9.23五年级奥数天天练
2011-09-26 16:28:46
标签:小升初真题
重庆奥数网奥数天天练栏目每日为大家转发中等、高等难度试题各一道。中难度试题适合一些有过思维基础训练、考 题学习经历,并且奥数成绩中上的学生。高难度试题立足于杯赛真题、综合应用和加深各知识点,适合一些志在竞赛中 夺取佳绩的学生。
本周试题由查字典奥数名师刘斌精选、解析,以保证试题质量。
难度:★★★★
(第二届小学迎春杯数学竞赛)有100位旅客,其中有10人既不懂英语又不懂俄语,有75人懂英语,83人懂俄语.问既懂英语又懂俄语的有多少人?
【答案】
方法一:在 人中懂英语或俄语的有:100-10=90(人).又因为有75人懂英语,所以只懂俄语的有:90-75=15(人).从83位懂俄语的旅客中除去只懂俄语的人,剩下的83-15(人)就是既懂英语又懂俄语的旅客.
方法二:学会把公式进行适当得变换,由包含与排除原理,得: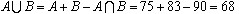 (人)
(人)
难度:★★★★★
在前100个自然数中,能被2或3整除的数有多少个?
【答案】
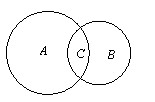
如图所示,A圆内是前100个自然数中所有能被2整除的数,B圆内是前100个自然数中所有能被3整除的数,C为前100 个自然数中既能被2整除也能被3整除的数.
前100个自然数中能被2整除的数有:100÷2=50(个).由100÷3=33…1知,前100个自然数中能被3整除的数有:33个.由100÷(2×3)=16…4知,前100个自然数中既能被2整除也能被3整除的数有16个.
所以A中有50个数,B中有33个数,C中有16个数.因为A,B都包含C ,根据包含排除法得到,能被2或3整除的数有:55+33-16(个).
查看全部
来源:查字典小升初网