小升初奥数试题及答案(十二)

二年级

1.找规律填数：5、6、1、7、8、5、3、8、1、9、()、()、()

2.已知○+□=24，□=○+○+○，那么○、□分别代表多少?

三年级

1.观察按一定规律排列的图形，○○□□□△△○○□□□△△○○□□□△△……，第50个图形是什么?

2.在一条水渠的一侧连两端共植树83棵，每两棵树之间间隔5米，这条水渠有多长?

四年级

1.在1—100中，所有除以6不余0的自然数的总和是多少?

2.规定a◎b=a+(a+1)+(a+2)+……+(a+b-1)，其中a、b都是自然数。计算1◎100。

五年级

1.某班同学在一次数学考试中，全班的平均成绩是90.5分，但后来发现在计算时，把一位同学的96分误看成了69分，经过重新计算后，全班的平均成绩是91分。全班共有多少位同学?

2.一个班的同学做数学竞赛题。第一次及格人数比不及格人数的3倍多4人，第二次及格人数增加了5人，这样，及格人数是不及格人数的6倍。全班共有多少人?

六年级

1.比较

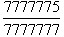和

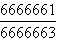的大小。 2.等式

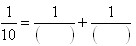中，括号内是两个不同的自然数，那么这两个数的和最小是多少?

二年级

1.找规律填数：5、6、1、7、8、5、3、8、1、9、()、()、()

解答：规律是从第三个数开始，每个数都是前两个数之和的个位数字。填0、9、9。

2.已知○+□=24，□=○+○+○，那么○、□分别代表多少?

解答：○+○+○+○=24，所以○=6，□=6+6+6=18。

三年级

1.观察按一定规律排列的图形，○○□□□△△○○□□□△△○○□□□△△……，第50个图形是什么?

解答：每7个图形是一组。50÷7=7……1，应该是○。

2.在一条水渠的一侧连两端共植树83棵，每两棵树之间间隔5米，这条水渠有多长?

解答：83棵树之间共有83-1=82个间隔。82×5=410(米)。

四年级

1.在1—100中，所有除以6不余0的自然数的总和是多少?

解答：除以6余0的数的总和很容易求出来，这样的数有6、12、18、……、96，共16个数。这些数的总和是(6+96)×16÷2=816。1—100这100个数的总和是(1+100)×100÷2=5050。从这100个数中去掉所有除以6余0的数即可，因此答案是5050-816=4234。

2.规定a◎b=a+(a+1)+(a+2)+……+(a+b-1)，其中a、b都是自然数。计算1◎100。

解答：a◎b的意思就是说，从a开始往后加，一共有b个数相加。那么1◎100的意思就是从1开始往后加，一共有100个相加。实际上1◎100就是1+2+3+……+100=5050。

五年级

1.某班同学在一次数学考试中，全班的平均成绩是90.5分，但后来发现在计算时，把一位同学的96分误看成了69分，经过重新计算后，全班的平均成绩是91分。全班共有多少位同学?

解答：96分比69分多27分，由于多出27分，就使平均成绩提高0.5分，也就是说全班每人平均提高0.5分，总分提高27分。27÷0.5=54(位)。

2.一个班的同学做数学竞赛题。第一次及格人数比不及格人数的3倍多4人，第二次及格人数增加了5人，这样，及格人数是不及格人数的6倍。全班共有多少人?

解答：因此第二次及格人数增加5人，那么不及格人数就减少5人。假如不及格人数减少5人，按第一次的计算，及格人数也随着减少5×3=15人，那么及格人数仍比不及格人数的3倍多4人，可事实上第二次的及格人数不仅没有减少，反而增加了5人。因此15+5+4=24人就对应着第二次不及格人数的6-3=3倍。第二次不及格人数是24÷3=8人，全班共有8×(1+6)=56人。

六年级