小升初奥数试题及答案(十八)
二年级
1.按图形变化的规律,在空格处画出相应的图形。
2.小红做题太粗心,减法当成加法题,25错看成52,算出的结果是130,正确的结果是多少?
三年级
1.100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
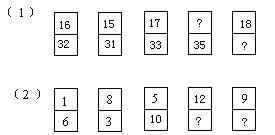
2.寻找规律填数:
 问:李得了几分?
问:李得了几分?
2.鸡兔同笼,兔比鸡多15只,脚数共228只,鸡、兔各几只?
四年级
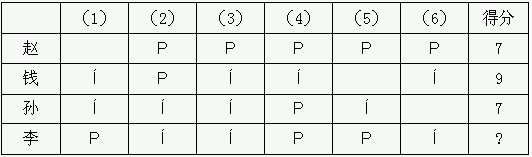
1.某次数学比赛,共有6道试题,都是是非题,正确的画“P”错误的画“??”每题答对得2分,不答得1分,答错得0分,赵、钱、孙、李的答案及前三人的得分如下表
 五年级
五年级
1.在7进制有三位数(ABC)7,把它化为9进制为(CBA)9,求这个三位数在十进制中为多少?
2.有一个数阵
 在表中第20行第19个数是多少?
在表中第20行第19个数是多少?
六年级
1.若干项货物总重量19.5吨,每箱重量不超过353千克,今有载重量为1.5吨的汽车,至少需要多少辆,才能把这些箱货物一次全部运走?
2.在下面一列数中,从第二个数开始,每个数都比他前面相邻的数大7。
8,15,22,29,36,43……它们前(N-1)个数相乘的积的末尾0的个数比前N个数相乘的积的末尾0的个数少3个,求N的最小值。
二年级
1.按图形变化的规律,在空格处画出相应的图形。
 解答:第四个图是15颗星。第二减第一等于3,第三减第二等于4,第四减第三等于5。他们的差都是1,也就是连续的自然数。
解答:第四个图是15颗星。第二减第一等于3,第三减第二等于4,第四减第三等于5。他们的差都是1,也就是连续的自然数。
2.小红做题太粗心,减法当成加法题,25错看成52,算出的结果是130,正确的结果是多少?
解答:根据条件,列出正确的算式及错误的算式。
正确:()-25=?
错误:()+52=130
由错误的算式求出正确的和,也就是正确算式中的被减数,再把它代入减法算式中,求出差。130-52=78,78-25=53
三年级
1.100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍。问:大、小和尚各有多少人?
解答:本题由中国古算名题“百僧分馍问题”演变而得。如果将大和尚、小和尚分别看作鸡和兔,馍看作腿,那么就成了鸡兔同笼问题,可以用假设法来解。
假设100人全是大和尚,那么共需馍300个,比实际多300-140=160(个)。现在以小和尚去换大和尚,每换一个总人数不变,而馍就要减少3-1=2(个),因为160÷2=80,故小和尚有80人,大和尚有100-80=20(人)。
同样,也可以假设100人都是小和尚,同学们不妨自己试试。
2.寻找规律填数:
 解答:(1)考察上、下两数的差。32-16=16,31-15=16,33-17=16,可知,上面那个“?”=35-16=19,下面那个“?”=18+16=34。
解答:(1)考察上、下两数的差。32-16=16,31-15=16,33-17=16,可知,上面那个“?”=35-16=19,下面那个“?”=18+16=34。
(2)从左至右,一上一下地看,由1,3,5,?,9,…知,12下面的“?”=7;一下一上看,由6,8,10,12,?,…知,9下面的“?”=14。
四年级
1.某次数学比赛,共有6道试题,都是是非题,正确的画“P”错误的画“??”每题答对得2分,不答得1分,答错得0分,赵、钱、孙、李的答案及前三人的得分如下表
 问:李得了几分?
问:李得了几分?
解答:由得分情况及答题量可知:钱对4错1,赵、孙各对3错2。
先看赵、钱有3题答案不同,所以两人的错题只能发生在3、4、6三道上,由此得到另三题的正确答案:(1)??(2)P(5)P。对照知,孙的(2)、(5)题答错了,所以其余已答题都对,得到(3)(4)题的正确答案:(3)??(4)P。因为钱只错1题,4题已错,故(6)题正确,为(6)??。对照正确答案,李对4道错2道,得8分。
2.鸡兔同笼,兔比鸡多15只,脚数共228只,鸡、兔各几只?
解答:假设兔与鸡的只数同样多。就可以去掉15只兔。
脚数共有:228-15??4=168(只)
鸡头与兔头相等,1只鸡和1只兔组成一组就有6只脚:2+4=6(只)
有多少组就有多少只鸡:168÷6=28(只)
有多少只兔:28+15=43(只)
五年级
1.在7进制有三位数(ABC)7,化为9进制为(CBA)9,求这个三位数在十进制中为多少?
解答:还原成十进制
49a+7b+c=a+9b+81c48a=80c+2b24a=40c+b
试验:b=0a=5c=3
(503)7=5×72+3=248
2.有一个数阵
 在表中第20行第19个数是多少?
在表中第20行第19个数是多少?
解答:仔细观察会发现:行数+列数-1=斜行数
第20行第19个数在第20+19-1=38斜行的第20个
第38斜行的第一个数是:37×38+1=1407
第38斜行的第20个数是:1407+19×2=1445
六年级
1.若干项货物总重量19.5吨,每箱重量不超过353千克,今有载重量为1.5吨的汽车,至少需要多少辆,才能把这些箱货物一次全部运走?
解答:19.5÷1.5=13,因此只需要13辆汽车就可以把这些货物一次全部运走。这就完全错了,因为货物是整箱装的,每辆汽车不一定都能载满。
15辆汽车不能保证一次运完。例如这批货物共有65只箱子,其中64只箱子的重量都是301千克,另1只箱子重量是236千克,总重量恰好是19500千克。由于301×5=1505(千克),即5只重量为301千克的箱子的总和超过1.5吨,因此每辆车最多只能装4箱重量为301千克的箱子,15辆最多只能装60箱重量为301千克的箱子,这样,必然有4只重量为301千克的箱子无法再运了。
16辆汽车可以保证一次运全部箱子。首先让12辆汽车装到刚刚超过1.5吨,即若取下最后装的一只箱子就不超过1.5吨。再从这12辆汽车上把每辆车最后装的那只箱子卸下来,并把这12只箱子分别装上另外3辆空车,每车4箱,由于每车4箱总重量不超过4×353=1412(千克),因此也不超过1.5吨,这时,12+3=15(辆)车就装完原来12辆汽车上的全部货物,总重量超过1.5×12=18吨,而且每辆车载重量不超过1.5吨。于是,剩下未装车的箱子总重量不足19.5-18=1.5(吨),所以16辆汽车可以一次运完全部货物。
2.在下面一列数中,从第二个数开始,每个数都比他前面相邻的数大7。
8,15,22,29,36,43……它们前(N-1)个数相乘的积的末尾0的个数比前N个数相乘的积的末尾0的个数少3个,求N的最小值。
解答:根据题意第N个数应当是53的倍数且不是54的倍数。第N个数是(7N+1),为使(7N+1)是5的倍数,N的个位数是2或7。经试验,当N=107时,7N+1=750=53×6,所以N最小107。