数论问题中数的整除问题练习题七
2011-08-01 21:20:48
标签:小升初真题

2位数进行改写。根据十进制数的意义,有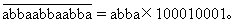
因为100010001各数位上数字之和是3,能够被3整除,所以这个12位数能被3整除。
根据能被7(或13)整除的数的特征,100010001与(100010-1=) 100009要么都能被7(或13)整除,要么都不能被7(或13)整除。
同理, 100009与( 100-9=)91要么都能被7(或13)整除,要么都不能被7(或13)整除。
因为91=7×13,所以100010001能被7和13整除,推知这个12位数能被7和13整除。

分析与解:根据能被7整除的数的特征,555555与999999都能被7
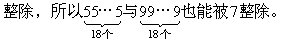
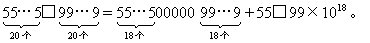
因为上式中等号左边的数与等号右边第一个数都能被7整除,所以等号右边第二个数也能被7整除,推知55□99能被7整除。根据能被7整除的数的特征,□99-55=□44也应能被7整除。由□44能被7整除,易知□内应是6。
下面再告诉大家两个判断整除性的小窍门。
判断一个数能否被27或37整除的方法:
对于任何一个自然数,从个位开始,每三位为一节将其分成若干节,然后将每一节上的数连加,如果所得的和能被27(或37)整除,那么这个数一定能被27(或37)整除;否则,这个数就不能被27(或37)整除。
查看全部
来源:查字典小升初网