2012年小升初数学模拟试卷及答案

2012年小升初数学模拟试卷

区、县________ 学校________ 姓名________ 得分_____

2012年小升初数学模拟试卷及答案，供小升初同学们练习。 更多小升初试题

一、计算题：（每题5分，共10分）

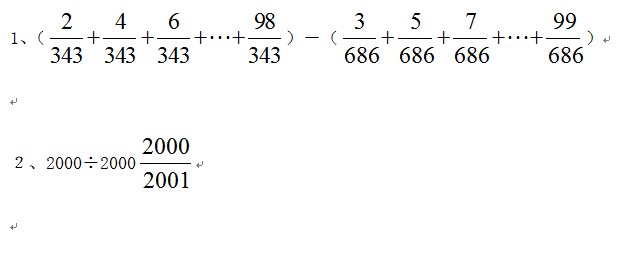
二、填空题（每题5分，共25分） （延伸阅读：小学六年级毕业班数学总复习概念文档免费下载）

１、某人乘车上班，因堵车，车速降低了20％，那么他在路上的时间增加了＿ ％

２、七个连续质数，从大到小排列为a，b，c，d，e，f,g。已知它们的和是偶数，那么c=__________

３、商店里有六箱货物，分别重15，16，18，19，20，31千克，两个顾客买走了其中的五箱。已知一个顾客买的货物重量是另一个顾客的2倍，那么商店剩下的一箱货物重量是______ 千克。

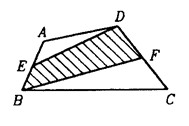
４如图所示：任意四边形ABCD，E是AB中点，F是CD中点，已知四边形ABCD面积是10，则阴影部分的面积是____________。

５、一个三位自然数正好等于它各数位上的数字和的18倍。这个三位自然数是_________。

三、解答题：（1~7题每题5分，8，9，10题每题10分，共65分）（延伸阅读：重点中学小升初语文模拟试卷及答案分析）

１、乙的速度是甲的速度的2/3。两人分别由A，B两地同时出发，如果相向而行1小时相遇；如果同向而行甲需多少小时才能追上乙？

２、甲乙两种商品，成本共2200元，甲商品按20％的利润定价，乙商品按15％的利润定价。后来都按定价的90％打折出售，结果仍获利131元。甲种商品的成本是多少元？

３、现在是11点整，再过多少分钟，时针和分针第一次垂直？

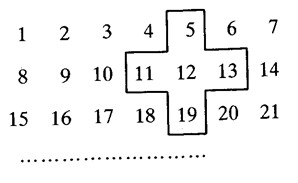
４、下图是一张把自然数按一定顺序排列的数表。用一个五个空格的十字框可以框出五个不同的数字，现框出的框内五个数字的四角上数字的和是48，如果框出的五个数字的四角的和是624时，四个角上的数分别是多少？

５、小花到少年活动中心去，步行需要小时。她走30分钟后改乘汽车，结果提前35分钟到达目的地。如果她一开始就乘汽车，那么可比步行提前多少分钟到达少年活动中心？

６、面值为5角和8角的邮票共30张，总价值18元，那么面值为5角的邮票有多少张？

７、平面上有100条直线，其中没有两条直线相互平行，也没有三条直线或三条以上直线相交于一点，平面上这100条直线共有交点多少个？

８、一列数1，1，2，3，5，8，13，21……从第三项开始每一项是前两项的和，此数列的第2000项除以8的余数是多少？

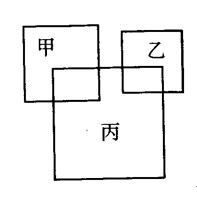
９、桌子上放有甲、乙、丙三个正方形，甲、丙有部分重叠，乙、丙有部分重叠。甲、丙重叠部分占甲正方形面积的1/4；乙、丙重叠部分占乙正方形面积的2/5。丙正方形与甲、乙正方形重叠部分占丙正方形面积的1/9。甲正方形和乙正方形面积的和是丙正方形面积的1/3。求：甲正方形面积与乙正方形面积的比。（要求化为最简整数比）

１０、三张卡片上分别标有p、q、r数码（整数）且0<p<q<r，游戏时将三张卡片随意分发给A、B、C三个人，每人各一张，根据每个人得到卡片上的数码分别给他们记分，如此重复游戏若干轮，结果A、B、C三人得分总数分别为20、10、9。已知B在最后一轮的得分是r，那么：

（1）_______在第一轮得分是q。

（2）p、q、r分别是_______、_________、_________。

数学、语文、英语小升初试题大奉送

小升初英语模拟试卷及答案

2010年育英中学初一分班考试题、小升初试题及答案

2012年小升初数学模拟试卷答案

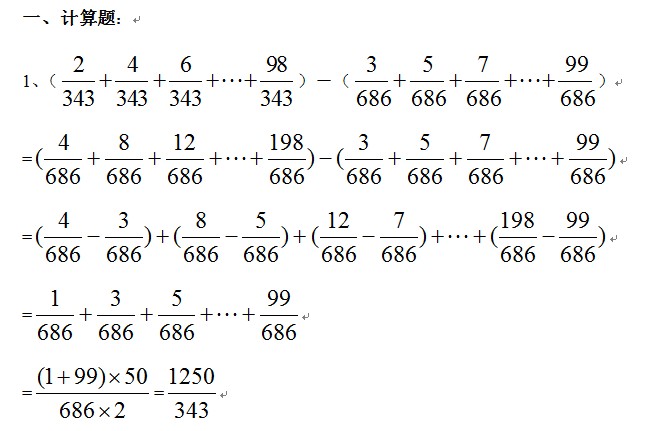
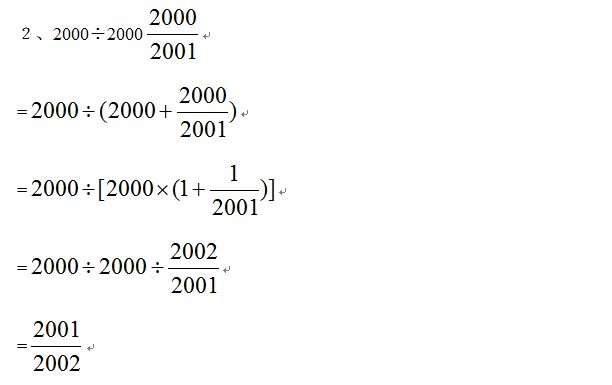
二、填空题

１、他在路上的时间增加了25%

解：设原来路程为5,车速为5,显然时间为1.现在车速降低了20%，则现在车速为5×（1-20%）＝4；时间为：5÷4＝1.25，增加了25%

２、c=11

解：7个连续质数，和是偶数，显然里面必然有2,又因为是从大到小排列的，所以依次可得到：g=2,f=3,e=5,d=7,c=11.

３、剩下的一箱只能是20千克的

解：因为一个顾客买的货物重量是另一个顾客的2倍，同时都是整数千克，所以他们买的货物和必定是3的倍数。即：他们买的货物的和能整除3.可以用余数性质：a与b的和除以c的余数等于a除以c的余数加上b除以c的余数的和除以c的余数。

15,16,18,19,20,31除以3的余数分别为0,1,0,1,2,1；而1+1+1能整除3,因此剩下的一箱只能是20千克的。

５、这个三位自然数是162

解：设这个自然数为ABC，由题意得：

100A+10B+C＝18（A+B+C）

化简得：82A＝8B+17C，因为B，C最多为9,因此82A最多为8×9+17×9＝225,即A只能为1或2.

当A＝1时，得82＝8B+17C，由B，C都是小于9的整数可得：B＝6,C＝2；

当A＝2时，得164＝8B+17C，得：B＝12,C＝4（舍去）。

所以这个三位数是162。

三、解答题：

１、如果同向而行甲需5小时才能追上乙

解：乙的速度是甲的速度的2/3，因此可以认为乙的速度为“2”,甲的速度为“3”,相向而行1小时相遇，则A，B两地相距为“5”；同向而行，所需时间为：5÷（3-2）＝5小时。

２、甲种商品的成本是1200元

解：设甲种商品的成本是x元，则乙种商品的成本是(2200-x)元

[(1+20%)x+(1+15%)(2200-x)]×90%=2200+131

X=1200

答：甲种商品的成本是1200元

４、四个角的数分别是149,155,157,163.

解：观察可发现：四角数字之和是中心数字的4倍，所以当和是624时，中心数字为：624÷4＝156；四角数字上下与中心数差7,左右与中心数差1,因此，四个角的数分别是149,155,157,163.

５、可比步行提前56分钟到达少年活动中心

解：1又(1/3)小时＝80分，她走了30分钟，还剩下50分钟的路，但乘车后提前35分钟，说明：走路50分钟＝乘车50-35＝15分钟；因此可得到走路与乘车的时间关系：50：15＝80：24

即乘车只需24分钟，比步行提前80-24＝56分钟到达。

６、面值为5角的邮票有20张

解：如果面值都是8角的邮票，应该有30×8＝240角，但现在有180角（18元），相差240-180＝60角。差的是因为将5角的当成了8角，因此一张就差3角。5角的邮票的张数就是：60÷3＝20张

７、平面上有100条直线，其中没有两条直线相互平行，也没有三条直线或三条以上直线相交于一点，平面上这100条直线共有交点多少个？

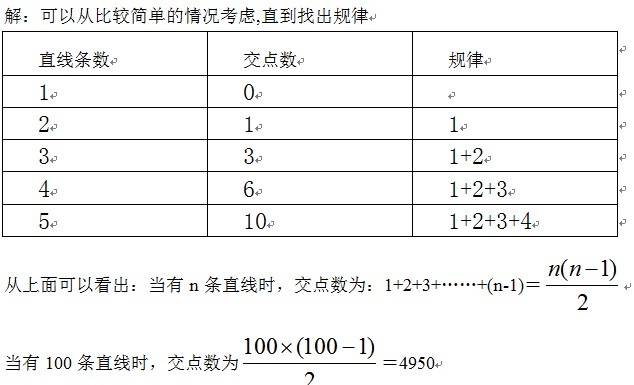
８、第2000项除以8的余数是5

解：数列的规律是：从第三项开始，每一项是前两项的和，因此由余数的性质：两数的和除以A的余数等于这两数分别除以A的余数的和再除以A的余数。可以写出余数的规律是：1,1,2,3,5,0,5,5,2,7,1,0,1,1,2,3,……它的循环周期是：1,1,2,3,5,0,5,5,2,7,1,0

2000÷12＝166……8,因此第2000项除以8的余数是5

９、甲乙面积比为4：5

解：设丙的面积是180（分母4,5,9,3的最小公倍数），则甲，乙面积和是180×(1/3)＝60,甲，乙和丙重叠的面积和是180×(1/9)＝20.

可用浓度问题来处理两者的关系：

60×(1/4)＝15，60×2(2/5)＝24

甲乙面积比为：（24-20）：（20-15）＝4：5

１０、（1）（ C ）在第一轮得分是q

（2）p,q,r分别是（1）、（4）、（8)

解：20+10+9=39=3*13 因为13轮不可能,因此只有3轮;那么,p+q+r=13;

可能的情况有:1 2 10 , 1 3 9, 1 4 8, 1 5 7, 2 3 8 , 2 4 7, 2 5 6, 3 4 6;

其中只有1 4 8 符合条件,p=1,q=4,r=8;第1轮A得8,第2轮得8,第3轮得4; 第1轮B得1,第2轮得1,第3轮得8;第1轮C得4,第2轮得4,第3轮得1

答:（1）（ C ）在第一轮得分是q

（2）p,q,r分别是（1）、（4）、（8).

数学、语文、英语小升初试题大奉送

小升初英语模拟试卷及答案

2010年育英中学初一分班考试题、小升初试题及答案