小学奥数牛吃草问题例题详解

牛吃草问题在普通工程问题的基础上，工作总量随工作时间均匀的变化，这样就增加了难度．牛吃草问题的关键是求出工作总量的变化率.

1. 草场有一片均匀生长的草地，可供27头牛吃6周，或供23头牛吃9周，那么它可供21头牛吃几周?(这类问题由牛顿最先提出，所以又叫“牛顿问题”．)

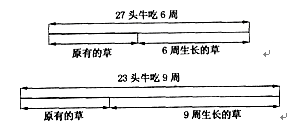
【分析与解】 27头牛吃6周相当于27×6=162头牛吃1周时间，吃了原有的草加上6周新长的草；

23头牛吃9周相当于23×9=207头牛吃1周时间，吃了原有的草加上9周新长的草；于是，多出了207-162=45头牛，多吃了9-6=3周新长的草．所以45÷3=15头牛1周可以吃1周新长出的草．即相当于给出15头牛专门吃新长出的草．于是27-15=12头牛6周吃完原有的草，现在有21头牛，减去15头吃长出的草，于是21-15=6头牛来吃原来的草；

所以需要12×6÷6=12(周)，于是2l头牛需吃12周．

评注：我们求出单位“1”面积的草需要多少头年来吃，这样就把问题化归为一般工程问题了．

一般方法：

先求出变化的草相当于多少头牛来吃：(甲牛头数×时间甲-乙牛头数×时间乙)÷(时间甲-时间乙)；

再进行如下运算：(甲牛头数-变化草相当头数)×时问甲÷(丙牛头数-变化草相当头数)=时间丙．

或者：(甲牛头数-变化草相当头数)×时间甲÷时间丙+变化草相当头数丙所需的头数．

2．有三块草地，面积分别是4公顷、8公顷和10公顷．草地上的草一样厚而且长得一样快．第一块草地可供24头牛吃6周，第二块草地可供36头牛吃12周．问：第三块草地可供50头牛吃几周?

【分析与解】 我们知道24×6=144头牛吃一周吃2个(2公顷+2公顷周长的草).36×12=432头牛吃一周吃4个(2公顷+2公顷12周长的草)．于是144÷2=72头牛吃一周吃2公顷+2公顷6周长的草．432÷4=108头牛吃一周吃2公顷+2公顷12周长的草．所以108-72=36头牛一周吃2公顷12—6=6周长的草．即36÷6=d头牛1周吃2公顷1周长的草．

对每2公顷配6头牛专吃新长的草，则正好．于是4公顷，配4÷2×6=12头牛专吃新长的草，即24-12=12头牛吃6周吃完4公顷，所以1头牛吃6×1÷(4÷2)=36周吃完2公顷．

所以10公顷，需要10÷2×6=30头牛专吃新长的草，剩下50-30=20头牛来吃10公顷草，要36 ×(10÷2)÷20=9周．

于是50头牛需要9周吃10公顷的草．

3．如图，一块正方形的草地被分成完全相等的四块和中间的阴影部分，已知草在各处都是同样速度均匀生长．牧民带着一群牛先在①号草地上吃草，两天之后把①号草地的草吃光．(在这2天内其他草地的草正常生长)之后他让一半牛在②号草地吃草，一半牛在③号草地吃草，6天后又将两个草地的草吃光．然后牧民把 的牛放在阴影部分的草地中吃草，另外号的牛放在④号草地吃草，结果发现它们同时把草场上的草吃完．那么如果一开始就让这群牛在整块草地上吃草，吃完这些草需要多少时间？

4．现在有牛、羊、马吃一块草地的草，牛、马吃需要45天吃完，于是马、羊吃需要60天吃完，于是牛、羊吃需要90天吃完，牛、羊一起吃草的速度为马吃草的速度，求马、牛、羊一起吃，需多少时间?

【分析与解】 我们注意到：

牛、马45天吃了 原有+45天新长的草① 牛、马90天吃了

2原有+90天新长的草⑤

马、羊60天吃了 原有+60天新长的草②

牛、羊90天吃了 原有+90天新长的草③

马 90天吃了 原有+90天新长的草④

所以，由④、⑤知，牛吃了90天，吃了原有的草；再结合③知，羊吃了90天，吃了90天新长的草，所以，可以将羊视为专门吃新长的草．

所以，②知马60天吃完原有的草，③知牛90天吃完原有的草．

现在将牛、马、羊放在一起吃；还是让羊吃新长的草，牛、马一起吃原有的草.

所需时间为l÷（1/60+1/90） =36天.

所以，牛、羊、马一起吃，需36天．

5. 有三片牧场，场上草长得一样密，而且长得一样快．它们的面积分别是3又1/3公顷、10公顷和24公顷．已知12头牛4星期吃完第一片牧场的草，21头牛9星期吃完第二片牧场的草，那么多少头牛18星期才能吃完第三片牧场的草?

【分析与解】 由于三片牧场的公顷数不一致，给计算带来困难，如果将其均转化为1公顷时的情形．

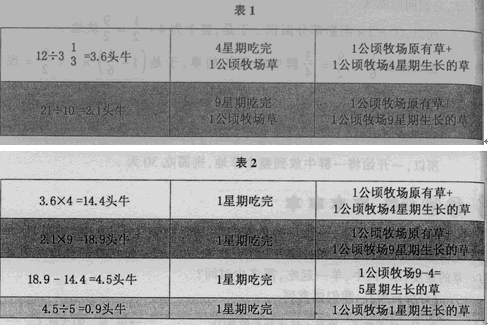
所以表1中，3.6-0.9=2.7头牛吃4星期吃完l公顷原有的草，那么18星期吃完1公顷原有的草需要2.7÷(18÷4)=0.6头牛，加上专门吃新长草的O．9头牛，共需0.6+0.9=1.5头牛，18星期才能吃完1公顷牧场的草．

所以需1.5×24=36头牛18星期才能吃完第三片牧场的草．

请下载附件：

小学奥数牛吃草问题例题详解

（共3页，本地下载在线阅读New！）