小升初奥数试题及答案(二)
二年级
1.下面一张数表中的数的排列存在某种规律,你能找出这个规律,并根据这个规律把括号里的数填上吗?
2 6 7 11
4 4 ( )1
3 5 5 6
2.树袋熊丫丫在爬一棵10米高的大树,每爬10分钟累了休息2分钟再继续爬,在这10分钟里它能向上爬2米。那么丫丫要多少分钟才能爬到树顶?
三年级
1.某人要到高层建筑的10层去,他从1层走到5层用了100秒,如果用同样的速度走到10层,则还需要多少秒?
2.某三对夫妇在一次聚会上相遇,他们是X,Y,Z先生和A,B,C女士,其中X先生的夫人和C女士的丈夫是初次见面,B女士的丈夫和A女士也是初次见面,Z先生认识所有的人。问:哪位先生和哪位女士是夫妇?
四年级
1.101个数之和为2008,把第一个数减1,第二个数加2,第三个数减3……第100个数加100,第101个数减101,则所得的101新数之和为多少?
2.将12个边长是1厘米的小正方形拼成一个长方形,其中周长最长的是多少厘米?最短的是多少厘米?
五年级
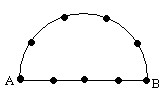
1.下面半圆图形上共有9个点,用这些点可以组成多少个三角形?
2.快慢两列火车相向而行,快车长50米,慢车长80米。快车速度是慢车的2倍,如果坐在慢车上的人见快车驶过窗口的时间是5秒。那么坐在快车上的人见慢车驶过窗口的时间是多少秒?
六年级
1.三个连续的自然数,从小到大依次是4、7、9的倍数,这三个自然数的和最小是多少?
2.三位数A满足:它的所有质因数之和是26。这样的三位数A有多少个?
1.下面一张数表中的数的排列存在某种规律,你能找出这个规律,并根据这个规律把括号里的数填上吗?
2 6 7 11
4 4 ( ) 1
3 5 5 6
解答:填3,规律是:上面两个数的和是下面的那个数的2倍。
2.树袋熊丫丫在爬一棵10米高的大树,每爬10分钟累了休息2分钟再继续爬,在这10分钟里它能向上爬2米。那么丫丫要多少分钟才能爬到树顶?
解答:10分钟能爬2米,那么要爬上10米的树,总共要爬10÷2=5(个)这样的10分钟,要花10×5=50(分钟)。在这期间,它要休息4次,需要2×4=8(分钟)。因此,丫丫要爬上这棵树,总共要花50+8=58(分钟)。
三年级
1.某人要到高层建筑的10层去,他从1层走到5层用了100秒,如果用同样的速度走到10层,则还需要多少秒?
解答:每上一层需要100÷(5-1)=25秒,所以还需要(10-5)×25=125秒。
2.某三对夫妇在一次聚会上相遇,他们是X,Y,Z先生和A,B,C女士,其中X先生的夫人和C女士的丈夫是初次见面,B女士的丈夫和A女士也是初次见面,Z先生认识所有的人。问:哪位先生和哪位女士是夫妇?
解答:Z不是C女士的丈夫,也不是B女士的丈夫,只能是A的丈夫。X先生的妻子不是C女士,所以X先生是B女士的丈夫,Y先生是C女士的丈夫。
四年级
1.101个数之和为2008,把第一个数减1,第二个数加2,第三个数减3……第100个数加100,第101个数减101,则所得的101新数之和为多少?
解答:所得的101个新数之和为:
2008-1+2-3+4-…-99+100-101=2008+-101=1957
2.将12个边长是1厘米的小正方形拼成一个长方形,其中周长最长的是多少厘米?最短的是多少厘米?
解答:拼成12×1的长方形周长最长,为(12+1)×2=26厘米;拼成4×3的长方形周长最短,为(4+3)×2=14厘米。
五年级
2.快慢两列火车相向而行,快车长50米,慢车长80米。快车速度是慢车的2倍,如果坐在慢车上的人见快车驶过窗口的时间是5秒。那么坐在快车上的人见慢车驶过窗口的时间是多少秒?
解答:快车速度+慢车速度=50÷5=10(米/秒),80÷10=8(秒)。
六年级
1.三个连续的自然数,从小到大依次是4、7、9的倍数,这三个自然数的和最小是多少?
解答:中间那个数是7的倍数,减1后是4的倍数,加1后是9的倍数。因此这个中间数除以4余1,除以9余8。通过实验发现,这个中间数最小是17,但要求这个数是7的倍数,所以这个数应该是17+36n(n是整数),满足条件的最小的n=4,那么中间数最小是17+36×4=161,这三个数的和最小是161×3=483。
2.三位数A满足:它的所有质因数之和是26。这样的三位数A有多少个?
解答:小于26的质因数有2、3、5、7、11、13、17、19、23。
若A的最大质因数是23,另一个质因数只能是3,A=23×3=69,不符合题意。
若A的最大质因数是19,那么其它质因数可以是7,2+2+3,2+5。A=19×7=133,A=19×2×2×3=228,A=19×2×5=190,有3个。
若A的最大质因数是17,那么其它质因数可以是2+2+2+3,2+2+5,2+7,3+3+3。A=17×2×2×2×3=408,A=17×2×2×5=340,A=17×2×7=238,A=17×3×3×3=458,有4个。
若A的最大质因数是13,那么其它质因数可以是13,2+2+2+2+2+3,2+2+2+2+5,2+2+2+7,2+2+3+3+3,2+3+3+5,2+11,3+3+7,3+5+5,满足条件的有A=13×2×2×3×3×3=728,13×2×11=286,13×3×3×7=819,13×3×5×5=975,13×13=169,有5个。
若A的最大质因数是11,那么其它质因数可以是2+2+2+2+2+2+3,2+2+2+2+2+5,2+2+2+2+7,2+2+2+3+3+3,2+2+3+3+5,2+2+11,2+3+3+7,2+3+5+5,只有A=11×2×2×11=484满足条件。
若A的最大质因数是7,那么剩下的质因数无论怎么拆分,乘积都大于999,因此这样的三位数有13个。